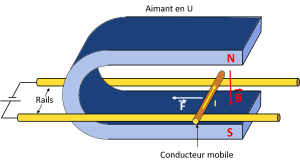
Principe de fonctionnement d'un moteur
Prérequis : force de Laplace (programme de physique)
Soit un conducteur mobile placé sur deux rails horizontaux connectés à un accumulateur qui fait circuler un courant dans ces deux rails et dans le conducteur mobile. Un aimant en U génère un champ magnétique. Le conducteur est alors sollicité par une force appelée force électromagnétique de Laplace notée \(\overrightarrow{F}\).
En notant :
\(\overrightarrow{B}\) le champ magnétique établi par l'aimant en U ;
\(i\) l'intensité du courant ;
\(\alpha\) l'angle de \(\overrightarrow{B}\) par rapport au conducteur ;
\(l\) la longueur du conducteur.
Alors, la force de Laplace est telle que \(\left\|\overrightarrow{F}\right\|=l\cdot i\cdot B \sin (\alpha)\)
Selon ce principe physique, il est possible de créer un actionneur, appelé moteur à courant continu qui transforme une puissance électrique en puissance mécanique au travers du déplacement en rotation d'une charge mécanique.
Le moteur à courant continu est formé d'un ensemble de boucle (l'induit) placée dans un champ magnétique constant que l'on suppose uniforme.
A l'aide d'une tension \(u(t)\) appliquée aux bornes de la boucle, on fait passer un courant continu \(i_a (t)\) dans la boucle. La présence du champ magnétique crée deux forces mécaniques de Laplace qui s'opposent sur cette boucle. Elle subit donc un couple (noté \(C_m (t)\)) qui la fait tourner. La figure ci-dessous montre le principe de fonctionnement sur une des boucles (source : www.energieplus-lesite.be).
Le couple \(C_m (t)\) est proportionnel à l'intensité du champ et à celle du courant dans la boucle, ce qui donne (si le champ magnétique est constant) : \(C_m (t)=k_m.i_a (t)\). La constante \(k_m\) est appelée la constante du couple moteur.
Cette boucle est en train de tourner. Le fait de tourner dans le champ magnétique constant génère une tension induite \(E(t)\) proportionnelle à l'intensité du champ et à la vitesse de rotation de la boucle : \(E(t)=k_e\cdot\omega_m (t)\)
La constante \(k_e\) est appelée constante contre-électromotrice et \(\omega_m (t)\) est la vitesse angulaire de rotation de l'arbre moteur (la boucle)
Lorsque le champ magnétique est constant, on a \(k_m=k_e=k\).
Lorsque ce moteur est chargé mécaniquement et en tenant compte du circuit électrique on obtient deux équations différentielles qui complètent le modèle de comportement du moteur (les démonstrations de ces deux équations seront vues plus tard en physique).
Fondamental : Équations d'un moteur à courant continu
Les équations régissant le fonctionnement d'une machine à courant continue commandée par une tension \(u\) et tournant à la vitesse \(\omega_m\) sont :
Les deux équations précédentes : \(C_m (t)=k_m.i_a (t)\) et \(E(t)=k_e\cdot\omega_m (t)\)
l'équation électrique : \(u(t)=R.i_a(t)+L_m\frac{di_a(t)}{dt}+E(t)\)
l'équation mécanique : \(J.\frac{d\omega_m(t)}{dt}=C_m(t)-f.\omega_m(t)\)
Avec :
\(k_m\) la constante du couple moteur,
\(k_e\) la constante contre-électromotrice,
\(J\) le moment d'inertie (\(kg.m^2\)),
\(L_m\) l'inductance de l'induit du moteur (\(H\)) ,
\(f\) le coefficient de frottement (\(Nm.s.rad^{-1}\)),
\(R\) la résistance de l'induit du moteur (\(\Omega\)).