Modèle du second ordre
Définition :
Un système d'entrée \(e(t)\) et de sortie \(s(t)\) est du second ordre, s'il est régi par une équation différentielle du second ordre à coefficients constants de la forme :
Avec :
\(K\) le gain du système (unité : [s]/[e]) ;
\(\omega_0\) la pulsation propre non amortie (unité : \(rad.s^{-1}\)), parfois noté \(\omega_n\), pulsation naturelle ;
\(\xi\) le coefficient d'amortissement du système (sans unité), parfois noté \(z\), \(m\),... ;
il est de plus nécessaire de donner deux conditions initiales, \(s(0\)) et \(\dot{s}(0)\) pour déterminer complètement le comportement du système. Par hypothèse, on se ramènera toujours en SI à des modèles tels que \(s(0)=\dot{s}(0)=0\)
Réponse indicielle (réponse à un échelon)
Fondamental :
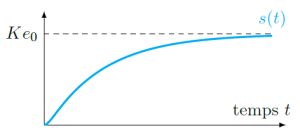
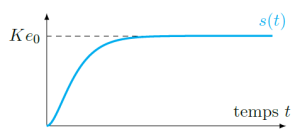
la réponse temporelle s(t) à une entrée en échelon \(e(t)=e_0.u(t)\) d'un système du second ordre présente toujours les caractéristiques suivantes :
la valeur finale \(s_\infty\) tend vers \(K.e_0\) sans dépassement ;
la pente de la tangente à l'origine est nulle.
Les autres caractéristiques de la réponse dépendent de la valeur du coefficient d'amortissement \(\xi\).
Il a été montré en cours de physique et il sera démontré en cours de mathématiques que la forme de la réponse temporelle (la partie transitoire de la réponse) dépend des racines du polynôme caractéristique associé à l'équation :
\(P(r)=\frac{1}{\omega_0^2}.r^2+\frac{2.\xi}{\omega_0} .r+1\) ou,plus simplement le polynôme équivalent \(P(r)=r^2+2.\xi.\omega_0.r+\omega_0^2\)
Le discriminant de ce polynôme vaut \(\Delta=4.\omega_0^2.(\xi^2-1)\). On distingue donc 3 cas en fonction des valeurs de \(\xi\) :
amortissement fort : \(\xi>1\), soit \(\Delta>0\), le polynôme présente 2 racines réelles ;
amortissement critique : \(\xi=1\), soit \(\Delta=0\), le polynôme présente 1 racine réelle double ;
amortissement faible : \(\xi<1\), soit \(\Delta<0\), le polynôme présente 2 racines complexes conjuguées.
Régime apériodique
Le régime apériodique correspond au cas où \(\xi>1\).
On montre que la solution complète de l'équation différentielle est de la forme :
\(s(t)=K.e_0\cdot\left(1-\frac{1}{T_1-T_2 }\cdot\left(T_1\cdot e^{-t/T_1}-T_2\cdot e^{t/T_2} \right)\right).u(t)\)
Avec \(T_1=\frac{1}{\xi.\omega_0+\omega_0.\sqrt{\xi^2-1}}\) et \(T_2=\frac{1}{\xi.\omega_0-\omega_0.\sqrt{\xi^2-1}}\)
Régime critique
Le régime critique correspond au cas où \(\xi=1\).
On montre que la solution complète de l'équation différentielle est de la forme :
\(s(t)=K.e_0.\left(1-\left(\omega_0.t+1\right).e^{-\omega_0.t} \right).u(t)\)
Régime pseudopériodique
Le régime pseudopériodique correspond au cas où \(\xi<1\).
On montre que la solution complète de l'équation différentielle est de la forme :
\(s(t)=K\cdot e_0\cdot\left(1-\frac{e^{-\xi.\omega_0.t}}{\sqrt{1-\xi^2 }} \sin\left(\omega_p\cdot t+\varphi\right) \right).u(t)\)
Avec \(\omega_p=\omega_0\cdot \sqrt{1-\xi^2}\) et \(\varphi= \arctan \left(\frac{\sqrt{1-\xi^2 }}{\xi}\right)\)
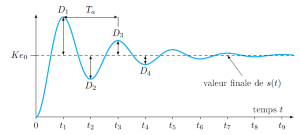
Du fait de la fonction sinusoïdale, le régime pseudopériodique présente toujours, en réponse à un échelon, un ou plusieurs dépassements (oscillations) caractérisés par :
\(\omega_p=\omega_0.\sqrt{1-\xi^2 }\), pseudo-pulsation et \(T_p=2\pi/\omega_p\) pseudo-période
Le kième dépassement relatif \(D_k (\%)\) est défini tel que : \(D_k (\%)=\left|\frac{s(t_k )-s_\infty}{s_\infty }\right|=e^{\left(-k\pi\xi/\sqrt{1-\xi^2 }\right)}\)
\(t_k\), temps du kième dépassement, tel que : \(t_k=\frac{k\pi}{\omega_0.\sqrt{1-\xi^2 }}=\frac{k\pi}{\omega_p}\)
Comme pour les systèmes du premier ordre, le paramètre caractéristique K influence la réponse en régime permanent (quand \(t \to \infty\)) uniquement. Les paramètres \(\xi\) et \(\omega_0\) influencent la réponse transitoire selon les figures ci-dessous.
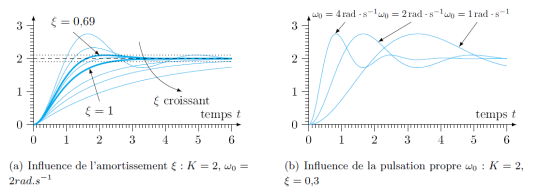
Remarque :
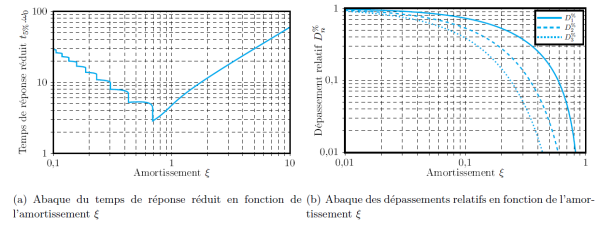
Dans le cas des systèmes du second ordre, il n'y a pas de relation analytique simple permettant de calculer le temps de réponse à 5%. On utilise alors un « abaque adimensionné », qui permet de lire le temps de réponse réduit (\(=t_{5\%}.\omega_0\) ) en fonction du coefficient d'amortissement. Cette courbe est valable pour tous les systèmes du second ordre standard
On peut remarquer que l'amplitude du kième dépassement ne dépend que du coefficient d'amortissement \(\xi\).
On trace alors un second abaque permettant de lire graphiquement cette valeur et d'éviter l'utilisation des formules données ci-dessus.
Les deux abaques sont donnés sur la figure suivante :
