Modèle du premier ordre
Définition :
Un système d'entrée \(e(t)\) et de sortie \(s(t)\) est du premier ordre, s'il est régi par une équation différentielle du premier ordre à coefficients constants de la forme :
avec :
\(\tau\) la constante de temps du système (unité : seconde) ;
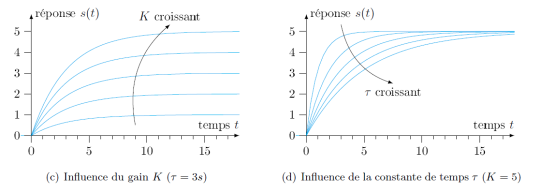
\(K\) le gain du système (unité : [s]/[e]) ;
il est de plus nécessaire de donner une condition initiale \(s(0)\) pour déterminer complètement le comportement du système. Par hypothèse, on se ramènera toujours en S.I à des modèles tels que \(s(0)=0\).
Réponse indicielle (réponse à un échelon)
Fondamental :
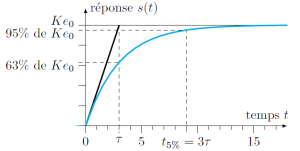
Cette réponse présente toujours les caractéristiques suivantes :
la valeur finale \(s_\infty\) tend vers \(K.e_0\) sans dépassement ;
la pente de la tangente à l'origine est non nulle ;
le temps de réponse à 5% vaut \(t_{5\%}=3.\tau\)
Le paramètre caractéristique K influence donc la réponse en régime permanent (quand \(t\to +\infty\)) et le paramètre \(\tau\) influence la réponse transitoire.