Hypothèses
Dans le cadre du cours de commande des systèmes de CPGE, l'étude se limite au systèmes linéaires, continus, invariants et mono-variables.
Définition : Système mono-variable
Un système mono-variable est un système ne possédant qu'une seule entrée et une seule sortie. Bien que les systèmes automatisés puissent gérer plusieurs sorties en fonction de plusieurs entrées principales, nous nous limiterons, pour des raisons de simplicité, aux systèmes mono-variables.
Si un système fonctionne avec plusieurs entrées (une consigne et une perturbation par exemple), chaque entrée aura son propre effet sur la sortie en cas de linéarité (cf. définition ci-dessous)
Définition : Système invariant
Les caractéristiques de comportement d'un système invariant sont indépendantes du temps. Si une même entrée se produit à deux instants distincts (\(t_1\) et \(t_2\)), alors les deux sorties temporelles \(s_1(t)\) et \(s_2(t)\) dues à chacune des deux entrées seront identiques.
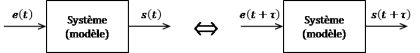
Définition : Système continu
Un système est à temps continu si les fonctions d'entrée et de sortie sont définies pour tout instant t. Les signaux sont alors dits analogiques.
Définition : Systèmes linéaires
Un modèle est dit linéaire si la sortie s(t) d'un système soumis à une combinaison linéaire d'entrées est égale à la même combinaison linéaire de la réponse à chacune de ces entrées.
Si \(e(t)=\sum_{i=1}^{n} \alpha_i.e_i(t)\) alors \(s(t)=\sum_{i=1}^n \alpha_i.s_i(t)\) avec \(s_i (t)\) la réponse du système à l'entrée \(e_i(t)\).
La relation de comportement d'un système linéaire peut se mettre sous la forme d'une équation différentielle linéaire à coefficients constants. Cette propriété sera à la base des développements ultérieurs.
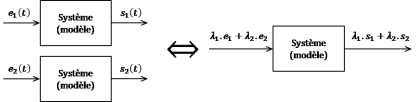
Définition : Théorème de superposition.
Soit un système linéaire, continu et invariant soumis à deux entrées, si ce système est soumis à deux entrées, alors chaque entrée aura son propre effet sur la sortie. Les deux entrée sont indépendantes et la présence d'une des entrées ne modifie pas l'effet de l'autre entrée.
La sortie sera alors la somme de l'effet de chacune des entrées.
Modèle
Comme nous l'avons vu dans le cycle 1, on peut représenter un système (ou un sous-système) sous la forme d'un bloc. Dans le premier chapitre, les diagrammes présentés permettaient de décrire un système ou de spécifier sa fonction, mais ils n'étaient pas utilisés pour simuler son comportement. Pour cela, il est nécessaire d'associer un modèle à chaque constituant, c'est-à-dire une ou plusieurs équations reliant les grandeurs d'entrées et de sorties du système. Dans le cadre du cours de commande des systèmes de CPGE, on ne travaille que sur des systèmes linéaires, continus et mono-variables. Les modèles utilisés sont donc des équations mathématiques linéaires reliant une unique fonction mathématique d'entrée \(e(t)\) et une unique fonction mathématique de sortie \(s(t)\).
Sous les hypothèses de continuité, de linéarité et d'invariance dans le temps, la relation de comportement d'un système peut toujours se mettre sous la forme d'une équation différentielle linéaire à coefficients constants.
On distingue deux types de modèles :
un modèle de connaissance, établi à partir de lois physiques permet d'aboutir généralement à une telle équation. Cette modélisation est analytique et possède un sens physique fort ;
à l'inverse, à partir d'un résultat expérimental sur tout ou partie du système, il est possible de proposer un modèle simple dit modèle de comportement d'un constituant. Il s'agit d'identifier.