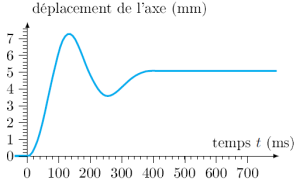
Identification second ordre
Soit la courbe de réponse en boucle ouverte mesurée un axe linéaire asservi en position. La longueur de consigne est un échelon d'amplitude \(e_0=5 mm\)
La courbe ci-contre indique la mesure de la position de l'axe en mm.
Question
Proposer un modèle de comportement de l'axe robot sous forme d'une équation différentielle à coefficients constants.
Solution
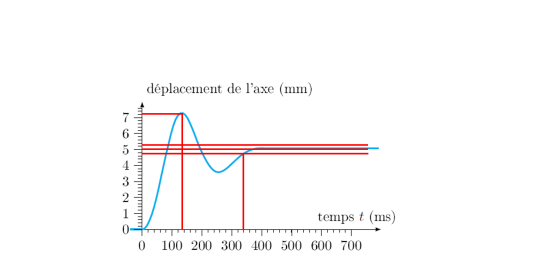
Le gain statique est \(K=1\).
La valeur relative du premier dépassement est \(D_1(\%)=\frac{7,2-5}{5}=44\%\), l'abaque nous donne le coefficient d'amortissement correspondant : \(\xi=0,25\).
L'instant du premier dépassement \(t_1=130ms\) permet d'obtenir \(\omega_0=\frac{\pi}{t_1\sqrt{1-\xi^2}}=25 \; rad.s^{-1}\).
Un résultat analogue peut être aussi trouver à l'aide de l'abaque : \(t_{5\%}\times \omega_0=10\) avec \(t_{5\%}=340ms\) donc \(\omega_0=\frac{10}{0,34}=29 \; rad.s^{-1}\)