Modélisation des entrées usuelles
Les signaux d'entrée du système peuvent correspondre à des fonctions quelconques du temps qui peuvent évoluer de façon prédéfinie (consignes définies par le cahier des charges) ou aléatoire (perturbations).
Afin de se donner un cadre d'étude et de comparaison, on définit un ensemble de signaux tests courants qui permettent d'établir le comportement d'un système et d'évaluer ses performances.
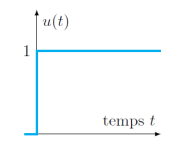
Échelon unité
Cette fonction modélise un signal qui passe de la valeur nulle à la valeur 1 très rapidement et qui reste ensuite constant et égal à 1.
Exemple : fermeture d'un interrupteur électrique.
La fonction échelon est définie par :
\(u(t)=\left\lbrace\begin{array}{c}0 \ \text{si} \ t<0 \\1 \ \text{si} \ t \geq 0 \\\end{array}\right.\)
Cette fonction respecte le principe de causalité, c'est-à-dire qu'elle est nulle pour les temps négatifs. En effet, l'ensemble des paramètres est supposé être au repos dans les temps négatifs.
Remarque :
Attention : ne pas confondre la notation u(t) avec la notion de tension électrique (souvent noté u(t) aussi).
Définition :
La réponse temporelle à un échelon est appelée réponse indicielle.
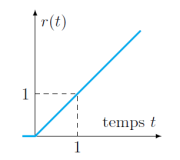
Rampe unitaire
Cette fonction modélise par exemple un déplacement imposé à vitesse constante.
La rampe de pente unitaire est définie par :
\(r(t)=\left\lbrace\begin{array}{c}0 \ \text{si} \ t<0 \\t \ \text{si} \ t \geq 0 \\\end{array}\right.\)
La fonction rampe peut s'exprimer à l'aide de la fonction échelon unitaire : \(r(t)=t.u(t)\)