Modélisation par un intégrateur
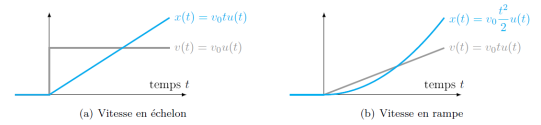
Une relation fondamentale lors de la modélisation des systèmes mécaniques est la relation permettant de passer de la vitesse \(v(t)\) à la position \(x(t)\) :
Il est souvent nécessaire d'établir la relation inverse, il faut alors intégrer :
Définition :
Un système est intégrateur s'il est défini par une relation de la forme :
avec \(K_I\) une constante.
Remarque :
Remarque : même si l'on parle de relation intégrale, on utilise souvent la forme dérivée entre les paramètres afin de faire apparaître des équations différentielles.
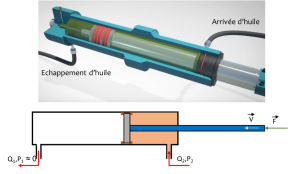
Exemple : Le vérin
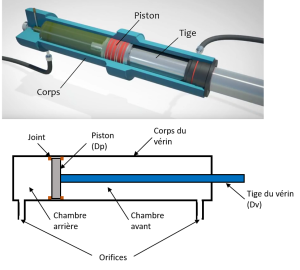
Tous deux sont de forme cylindrique. On note \(D_p\) le diamètre du piston et \(D_v\) le diamètre de la tige (cf. figure ci-contre et ci-dessous).
Pour faire sortir la tige, on amène du fluide sous pression sur la face arrière du piston :

Lors du déplacement de la tige le fluide entre dans la chambre avec un débit Q qui correspond à la variation du volume de la chambre en fonction du temps :
Cette variation de volume peut aussi s'exprimer par le produit de la section S du piston avec la variation de position de la tige \(\Delta x\) (donc du piston) : \(\Delta V=S.\Delta x\)
\(Q=\frac{S\cdot\Delta x}{\Delta t} \underset{\Delta t\to 0}{\longrightarrow} S\frac{dX}{dt}=S\cdot V_{tige}\) avec \(V_{tige}\) la vitesse de translation de la tige du vérin.
Fondamental :
Vitesse de déplacement de la tige du vérin et position de la tige du vérin en fonction du débit :