Utilisation de la fonction de transfert d'un système pour déterminer ses performances
Nous étudierons dans ce paragraphe les performances du système asservi décrit par le schéma bloc ci-dessous :
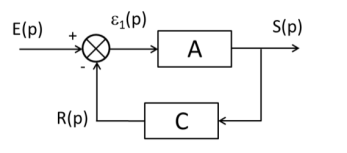
Sa fonction de transfert en boucle fermée \(H_{BF} (p)\) est telle que :
Cette fonction de transfert étant une fraction rationnelle de deux polynômes, il est possible de l'exprimer sous la forme :
On rappelle que les pôles de H(p) sont les valeurs \(p_i\) qui annulent le dénominateur. (Ce sont les racines de \(D(p)\))
Fondamental : Énoncé mathématique du critère de stabilité :
Un système asservi est stable si et seulement si sa fonction de transfert en boucle fermée possède UNIQUEMENT des pôles à partie réelle STRICTEMENT négative.
Définition :
La précision d'un système est la valeur vers laquelle tend l'écart \(\epsilon(t)\), résultat de la comparaison entre la consigne \(e(t)\) et le signal de retour \(r(t)\) quand \(t\to +\infty\). D'où l'expression de la précision en régime permanent \(\epsilon_S\) :
\(\epsilon_S=\lim\limits_{ t\to +\infty} \epsilon(t)=\lim\limits_{ t\to +\infty} \left(e(t)-r(t)\right)\)
Fondamental :
Cet écart peut être facilement déterminé à partir de l'expression de la fonction de transfert \(H(p)\) du système, si le système est stable, le théorème de la valeur finale peut être utilisé :
\(\epsilon_S=\lim \limits_{ t\to +\infty} \epsilon(t)=\lim\limits_{ p\to 0} p.\epsilon(p)=\lim\limits_{ p\to 0}\left(p\left[E(p)-R(p)\right]\right)\)
Or, \(R(p)=S(p).C(p)\) et \(\frac{S(p)}{E(p)} =H(p)\), d'où :
\(\epsilon_S=\lim\limits_{ p\to 0}p.E(p)\left[1-H(p).C(p)\right]\)
On peut noter que l'expression de la précision du système dépend de l'entrée \(E(p)\) qui lui est appliquée. On distingue généralement deux performances de précision :
L'erreur statique (\(\epsilon_{0}\)) : erreur statique du système en réponse à une consigne de type échelon. Pour l'exprimer, il suffit de remplacer la fonction \(E(p\)) par son expression \(E(p)=\frac{e_0}{p}\). L'erreur indicielle est souvent donnée en pourcentage relativement à l'amplitude de l'échelon d'entrée : \(\epsilon_0\%=\frac{\epsilon_0}{e_0}\cdot 100\).
L'erreur de traînage ou de poursuite (\(\epsilon_{1}\)) : erreur statique du système en réponse à une consigne en rampe. Pour l'exprimer, il suffit de remplacer la fonction \(E(p)\) par son expression \(E(p)=\frac{e_0}{p^2}\)
Remarque :
Dans certains cas, lorsque le système le permet, il est possible de déterminer la précision d'un système à partir de la comparaison entre la sortie du système et la valeur de la consigne lui ayant été appliquée. Cependant, il faut être vigilant et seules des grandeurs physiques de même nature peuvent être comparées. Ceci est particulièrement vrai dans le cas d'un système à retour unitaire, comme le montre l'exemple suivant.

Si les grandeurs physiques \(e(t)\) et \(s(t)\) sont identiques, il est possible de les comparer, et donc de déterminer l'erreur du système :
\(\epsilon_S=\lim\limits_{ t\to +\infty}\left(e(t)-s(t)\right)=\lim\limits_{ p\to 0}p.\left(E(p)-S(p)\right)\)
Soit : \(\epsilon_S=\lim\limits_{ p\to 0}p.E(p)-\lim\limits_{ p\to 0}p.S(p)\)
