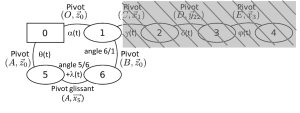
Cas du manège à sensations
On étudie ici la chaîne fermée constituée par les solides 0-1-5-6 possède une seule mobilité, c'est à dire qu'il n'existe qu'un seul mouvement indépendant dans cette boucle : si on bloque un des degrés de liberté d'une des liaisons, tous les autres degrés de libertés sont bloqués.
Mathématiquement, cela se traduit par le fait qu'il est possible d'exprimer 3 paramètres géométriques (angle de rotation dans la liaisons 5/0, \(\theta\), angle de rotation dans la liaison 6/1 (non nommé) et translation dans la liaison 5/6, \(\lambda\)) en fonction du quatrième (\(\alpha\), angle de rotation dans la liaison 1/0).
Question
En écrivant une relation de fermeture géométrique sur le cycle O-A-B-O, exprimer une relation entre l'angle \(\alpha\) paramétrant la rotation du solide 1 par rapport au sol 0 et la longueur \(\lambda\) paramétrant la translation du solide 6 par rapport au solide 5.
Étape 1 : écrire une relation de fermeture vectorielle ;
Étape 2 : en projetant cette relation vectorielle sur les axes \(\vec{x_0}\) et \(\vec{y_0}\) en déduire deux relations scalaires entre les différents paramètres ;
Étape 3 : utiliser ces deux relations pour faire apparaître la loi Entrée/Sortie demandée (\(\alpha=f(\lambda)\)).
Solution
Etape 1 : \(\vec{OA}+\vec{AB}+\vec{BO}=\vec{0}\) d'où \(a.\vec{x_0}+\lambda.\vec x_5-b.\vec{x_1}=\vec{0}\)
Etape 2 : projection sur \(\vec{x_0}\) donne \(a+\lambda.cos\theta-b.cos\alpha=0\)
projection sur \(\vec{y_0}\) donne \(\lambda.sin\theta-b.sin\alpha=0\)
Etape 3 : on veut faire disparaitre l'angle \(\theta\) et exprimer \(\lambda\) en fonction de \(\alpha\)
Réécriture de la première relation : \(b.cos\alpha-a=\lambda.cos\theta\)
Réécriture de la seconde relation : \(b.sin\alpha=\lambda.sin\theta\)
On passe les deux relations au carré et on les somme, en remarquant que \(cos\theta^2+sin\theta^2=1\)
On obtient alors la relation suivante : \(\lambda^2=(b.cos\alpha-a)^2+(b.sin\alpha)^2\)
C'est bien la relation qui était demandée (racine carré de la relation pour obtenir l'expression de \(\lambda\) si besoin.