Système sur-amorti : régime apériodique
Lorsque \(\xi>1\), le dénominateur possède deux racines réelles.
La forme canonique de la fonction de transfert devient :
2 pôles réels :
\(p_1=\omega_0(-\xi+\sqrt{\xi^2-1})\)
\(p_2=\omega_0(-\xi-\sqrt{\xi^2-1})\)
Auxquels correspondent 2 constantes de temps :
\(\tau_1=-\frac{1}{p_1}=\frac{1}{\omega_0(\xi-\sqrt{\xi^2-1})}\)
\(\tau_2=-\frac{1}{p_2}=\frac{1}{\omega_0(\xi+\sqrt{\xi^2-1})}\)
Remarque :
Un système du second ordre possédant un coefficient d'amortissement \(\xi > 1\) peut être considéré comme le produit de deux systèmes du premier ordre de temps caractéristiques \(\tau_1 = −1/ p_1\) et \(\tau_2 = −1/ p_2\) avec \(p_1\) et \(p_2\) les pôles de la fonction de transfert du second ordre.
La réponse du système à l'entrée en échelon non unitaire dans le domaine de Laplace s'écrit donc :
\(S(p)=\frac{e_0}{p}\cdot\frac{K}{(1+\tau_1\cdot p)(1+\tau_2\cdot p)}\)
Par décomposition en éléments simples puis par identification des transformées inverses, on obtient :
Remarque :
La réponse est la somme d'une constante représentant la réponse permanente et de deux exponentielles représentant les réponses transitoires. Selon les valeurs respectives des temps de réponse \(\tau_1\) et \(\tau_2\), l'influence de l'une de ces deux réponses transitoires peut parfois être négligeable.
Méthode : Prévoir la réponse indicielle à partir de la F.T
Vérifier l'ordre de la F.T.
Mettre sous forme canonique la F.T : \(H(p)=\frac{K}{1+\frac{2\cdot \xi}{\omega_{0}}\cdot p+\frac{p^2}{\omega_{0}^{2}}}\)
Identifier \(\xi\) et vérifier \(\xi>1\)
Mettre la F.T sous la forme canonique \(H(p)=\frac{K}{(1+\tau_1\cdot p)(1+\tau_2\cdot p)}\) pour identifier les constantes de temps.
Identifier K et en déduire la valeur finale : \(s_\infty=K.e_0\)
Identifier la pulsation propre \(\omega_0\) et en déduire le temps de réponse à \(5\%\) à l'aide de l'abaque ci-dessous qui donne le temps de réponse réduit (\(tr_{5\%}\cdot\omega_0\)) en fonction de \(\xi\).
Connaître l'allure de la courbe. (Pente nulle à l'origine).
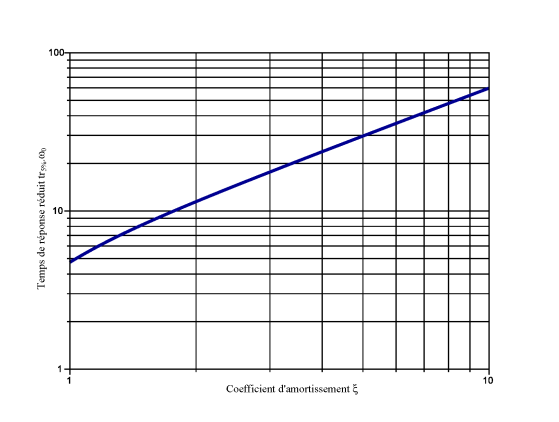
Remarque :
On ne peut pas identifier une F.T à partir d'une réponse indicielle pour \(\xi>1\) avec cet abaque. L'abaque nécessite de connaître soit la valeur de \(\xi\), soit la valeur de \(\omega_0\).
Il existe toutefois d'autres méthodes et abaques permettant d'identifier ces F.T.
Fondamental : Cas où l'une des constantes de temps est beaucoup plus grande que l'autre
SI \(\tau_1\gg\tau_2\), dans ce cas c'est la constante de temps la plus grande qui l'emporte. Il est alors possible d'avoir une approximation du temps de réponse à \(5\%\) : \(t_{r5\%}\simeq 3\tau_1\).
De plus, la fonction de transfert peut être approximée par une F.T du premier ordre :
\(H(p)\simeq\frac{K}{1+\tau_1.p}\)
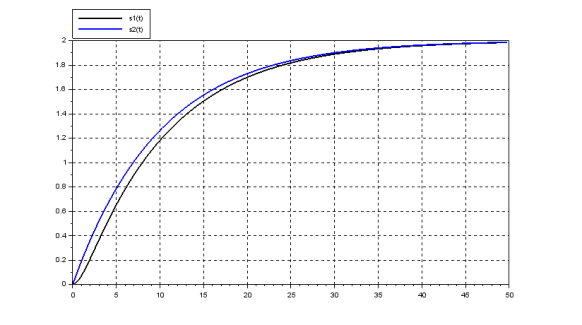
Exemple :
Tracés des réponses indicielle de \(H_1(p)=\frac{2}{(1+10\cdot p)\cdot(1+ p)}\) et \(H_2(p)=\frac{2}{(1+10\cdot p)}\) pour un échelon unitaire.