Liaisons en série.
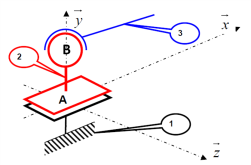
Soit le schéma cinématique ci-contre.
Question
Tracer le graphe des liaisons du mécanisme.
Solution

\(L_{12}\) : Liaison appui plan de normale \((A,\vec{y})\)
\(L_{23}\) : liaison sphérique (rotule)de centre B.
Question
Écrire les torseurs cinématiques de chaque liaison.
Solution
\(L_{12}\) : \(\left\{ \mathcal{V}_{2 1} \right\}=\left\{ \begin{array}{cc} 0 & V_{Ax}\\\omega_{21y} & 0 \\0 & V_{Az}\end{array}\right\}_{A,B}\)
\(L_{23}\) : \(\left\{ \mathcal{V}_{32} \right\}=\left\{ \begin{array}{cc} \omega_{32x} & 0\\\omega_{32y} & 0 \\\omega_{32z} & 0\end{array}\right\}_{B,B}\)
Question
Déterminer la liaison équivalente.
Solution
Les liaisons sont en série donc :
\(\left\{ \mathcal{V}_{eq} \right\}=\left\{ \mathcal{V}_{32} \right\}+\left\{ \mathcal{V}_{21} \right\}\)
Déplacement du torseur de la liaison 1-2 en B :
\(\overrightarrow{V} \left(B \in 2/1 \right)=\overrightarrow{V} \left(A \in 2/1\right)+\overrightarrow{BA} \wedge \overrightarrow{\Omega} \left(2/1 \right)=\overrightarrow{V} \left(A \in 2/1\right)\) car \(\overrightarrow{BA}\) est colinéaire à \(\overrightarrow{\Omega} \left(2/1 \right)\)
On en déduit :
\(\left\{ \mathcal{V}_{eq} \right\}=\left\{ \begin{array}{cc} \omega_{32x} & 0\\\omega_{32y} & 0 \\\omega_{32z} & 0\end{array}\right\}_{B,B}+\left\{ \begin{array}{cc} 0 & V_{Ax}\\\omega_{21y} & 0 \\0 & V_{Az}\end{array}\right\}_{B,B}=\left\{ \begin{array}{cc} \omega_{32x} & V_{Ax}\\\omega_{32y}+\omega_{21y} & 0 \\\omega_{32z} & V_{Az}\end{array}\right\}_{A,B}\)
On retrouve la forme du torseur cinématique d'une liaison ponctuelle de normale \((B,\vec{y})\)