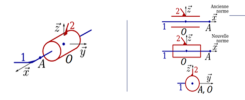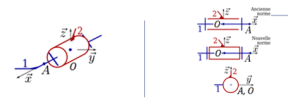Tableau des liaisons normalisées
Les liaisons les plus courantes rencontrées en construction mécanique sont normalisées par l'AFNOR. À chaque liaison sont associés un nom et une schématisation. Ces schématisations sont nécessaires pour établir, par exemple, le schéma cinématique d'un mécanisme.
Les hypothèses sont les suivantes :
les solides \(S_i\) et \(S_k\) sont indéformables et en mouvement relatif,
les surfaces de liaison entre les deux solides \(S_i\) et \(S_k\) sont géométriquement parfaites et leur positionnement géométrique relatif parfait,
les solides \(S_i\) et \(S_k\) sont en contact sans aucun jeu,
un repère \(R(O,\overrightarrow{X} ,\overrightarrow{Y} ,\overrightarrow{Z})\) est associé à chaque liaison.
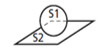
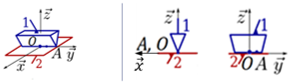
Liaison rotule (ou liaison sphérique)
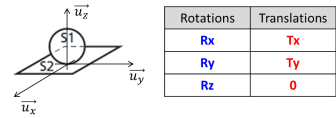
Une liaison rotule de centre O permet trois mouvements de rotation entre deux solides \(S_i\) et \(S_k\).
Nom | Liaison rotule (ou sphérique) |
|---|---|
Surfaces de contact | Sphère/sphère : |
Degrés de liberté | 3 rotations |
Schématisation |
|
Torseur cinématique associé | \(\left\{ \mathcal{V} \left( S_k / S_i \right)\right\}=\left\{ \begin{array}{c}\overrightarrow{\Omega} \left(S_k/S_i \right)=\omega_x\cdot \overrightarrow{X}+\omega_y\cdot \overrightarrow{Y}+\omega_z\cdot \overrightarrow{Z}\\\overrightarrow{V} \left(O \in S_k/S_i \right)= \overrightarrow{0}\end{array}\right\}_O=\left\{ \begin{array}{cc} \omega_x & 0\\\omega_y & 0 \\\omega_z & 0\end{array}\right\}_{O,B}\) |
Validité de la forme canonique du torseur | Point O, centre des sphères |
Liaison ponctuelle (ou liaison sphère-plan)
Une liaison ponctuelle de centre 0 et de normale \(\overrightarrow{Z}\) permet entre deux solides \(S_i\) et \(S_k\) :
deux mouvements de translation respectivement suivant deux axes perpendiculaires \((O,\overrightarrow{X})\) et \((O,\overrightarrow{Y})\),
trois mouvements de rotation respectivement autour des axes \((O,\overrightarrow{X})\), \((O,\overrightarrow{Y})\) et \((O,\overrightarrow{Z})\),
Nom | Liaison ponctuelle (liaison sphère-plan) |
|---|---|
Surfaces de contact | Sphère/plan : |
Degrés de liberté | 2 translations et 3 rotations |
Schématisation |
|
Torseur cinématique associé | \(\left\{ \mathcal{V} \left( S_k / S_i \right)\right\}=\left\{ \begin{array}{c}\overrightarrow{\Omega} \left(S_k/S_i \right)=\omega_x\cdot \overrightarrow{X}+\omega_y\cdot \overrightarrow{Y}+\omega_z\cdot \overrightarrow{Z}\\\overrightarrow{V} \left(O \in S_k/S_i \right)=V_x\cdot \overrightarrow{X}+V_y\cdot \overrightarrow{Y}\end{array}\right\}_O=\left\{ \begin{array}{cc} \omega_x & V_x\\\omega_y & V_y \\\omega_z & 0\end{array}\right\}_{O,B}\) |
Validité de la forme canonique du torseur | En tout point de l'axe \((O,\overrightarrow{Z})\) . |
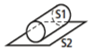
Liaison linéaire annulaire (ou liaison sphère-cylindre)
Une liaison linéaire annulaire de centre O et d'axe \((O,\overrightarrow{X})\) permet entre deux solides \(S_i\) et \(S_k\) :
un mouvement de translation suivant l'axe \((O,\overrightarrow{X})\),
trois mouvements de rotation respectivement autour des axes \((O,\overrightarrow{X})\), \((O,\overrightarrow{Y})\) et \((O,\overrightarrow{Z})\),
Nom | Liaison linéaire annulaire (liaison sphère-cylindre) |
|---|---|
Surfaces de contact | Sphère/cylindre : |
Degrés de liberté | 1 translation et 3 rotations |
Schématisation |
|
Torseur cinématique associé | \(\left\{ \mathcal{V} \left( S_k / S_i \right)\right\}=\left\{ \begin{array}{c}\overrightarrow{\Omega} \left(S_k/S_i \right)=\omega_x\cdot \overrightarrow{X}+\omega_y\cdot \overrightarrow{Y}+\omega_z\cdot \overrightarrow{Z}\\\overrightarrow{V} \left(O \in S_k/S_i \right)=V_x\cdot \overrightarrow{X}\end{array}\right\}_O=\left\{ \begin{array}{cc} \omega_x & V_x\\\omega_y & 0 \\\omega_z & 0\end{array}\right\}_{O,B}\) |
Validité de la forme canonique du torseur | Point O, centre de la sphère. |
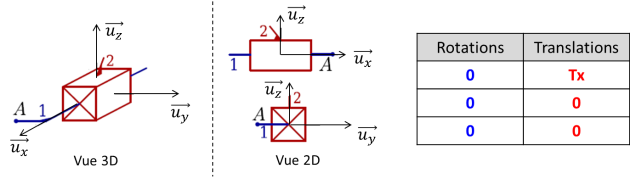
Liaison pivot glissant
Une liaison pivot glissant d'axe \((O,\overrightarrow{X})\) permet un mouvement de rotation autour de cet axe, et un mouvement de translation le long de cet axe entre deux solides \(S_i\) et \(S_k\). Les mouvements de rotation et de translation sont indépendants.
Nom | Liaison pivot glissant |
|---|---|
Surfaces de contact | Sphère/sphère : |
Degrés de liberté | 1 translation et 1 rotation. |
Schématisation | |
Torseur cinématique associé | \(\left\{ \mathcal{V} \left( S_k / S_i \right)\right\}=\left\{ \begin{array}{c}\overrightarrow{\Omega} \left(S_k/S_i \right)=\omega_x\cdot \overrightarrow{X}\\\overrightarrow{V} \left(O \in S_k/S_i \right)=V_x\cdot \overrightarrow{X}\end{array}\right\}_O=\left\{ \begin{array}{cc} \omega_x & V_x\\0 & 0 \\0 & 0\end{array}\right\}_{O,B}\) |
Validité de la forme canonique du torseur | Valable en tout point de l'axe \((O,\overrightarrow{X})\) (donc en A) |
Liaison linéaire rectiligne (ou liaison cylindre-plan)
Une liaison linéaire rectiligne d'axe \((O,\overrightarrow{Y})\) et de normale \(\overrightarrow{Z}\) permet entre deux solides \(S_i\) et \(S_k\) :
deux mouvements de translation respectivement suivant deux axes perpendiculaires \((O,\overrightarrow{X})\) et \((O,\overrightarrow{Y})\) ,
deux mouvements de rotation respectivement autour des axes \((O,\overrightarrow{Y})\) et \((O,\overrightarrow{Z})\) ,
Nom | Liaison linéaire rectiligne |
|---|---|
Surfaces de contact | Cylindre/plan : |
Degrés de liberté | 2 translations et 2 rotations |
Schématisation |
|
Torseur cinématique associé | \(\left\{ \mathcal{V} \left( S_k / S_i \right)\right\}=\left\{ \begin{array}{c}\overrightarrow{\Omega} \left(S_k/S_i \right)=\omega_y\cdot \overrightarrow{Y}+\omega_z\cdot \overrightarrow{Z}\\\overrightarrow{V} \left(O \in S_k/S_i \right)=V_x\cdot \overrightarrow{X}+V_y\cdot \overrightarrow{Y}\end{array}\right\}_O=\left\{ \begin{array}{cc} 0 & V_x\\\omega_y & V_y \\\omega_z & 0\end{array}\right\}_{O,B}\) |
Validité de la forme canonique du torseur | Valable en tout point du plan \((0,\overrightarrow{Y},\overrightarrow{Z})\). |
Liaison appui plan
Une liaison appui plan de normale \(overrightarrow{Z}\) permet entre deux solides \(S_i\) et \(S_k\) :
deux mouvements de translation respectivement suivant deux directions perpendiculaires \(\overrightarrow{X}\) et \(\overrightarrow{Y}\) ,
un mouvement de rotation autour de la direction \(\overrightarrow{Z}\).
Nom | Liaison appui plan |
|---|---|
Surfaces de contact | Sphère/sphère : |
Degrés de mobilité liberté | 2 translations et 1 rotations |
Schématisation |
|
Torseur cinématique associé | \(\left\{ \mathcal{V} \left( S_k / S_i \right)\right\}=\left\{ \begin{array}{c}\overrightarrow{\Omega} \left(S_k/S_i \right)=\omega_z\cdot \overrightarrow{Z}\\\overrightarrow{V} \left(A \in S_k/S_i \right)=V_x\cdot \overrightarrow{X}+V_y\cdot \overrightarrow{Y}\end{array}\right\}_A=\left\{ \begin{array}{cc} 0 & V_x\\0 & V_y \\\omega_z & 0\end{array}\right\}_{A,B}\) |
Validité de la forme canonique du torseur | Valable en tout point de l'espace. |
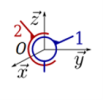
Liaison pivot
Une liaison pivot d'axe \((O,\overrightarrow{X})\) permet un mouvement de rotation, autour de cet axe, entre deux solides \(S_i\) et \(S_k\).
Nom | Liaison pivot |
|---|---|
Association de liaisons élémentaires | Rotule + linéaire annulaire. Pivot glissant + appui plan ... |
Degrés de mobilité (liberté) | 1 rotation |
Schématisation | |
Torseur cinématique associé | \(\left\{ \mathcal{V} \left( S_k / S_i \right)\right\}=\left\{ \begin{array}{c}\overrightarrow{\Omega} \left(S_k/S_i \right)=\omega_x\cdot \overrightarrow{X}\\\overrightarrow{V} \left(O \in S_k/S_i \right)=\overrightarrow{0}\end{array}\right\}_O=\left\{ \begin{array}{cc} \omega_x & 0\\0 & 0 \\0 & 0\end{array}\right\}_{O,B}\) |
Validité de la forme canonique du torseur | Valable en tout point de l'axe \((O,\overrightarrow{X})\) (donc en A) |
Le torseur caractéristique de cette liaison est un torseur Glisseur.
Remarque : en tout point \(I\) de l'axe \((O,\overrightarrow{X})\) d'une liaison pivot \(\overrightarrow{V} \left(I \in S_k/S_i \right)=\overrightarrow{0}\).
Liaison glissière
Une liaison glissière de direction \(\overrightarrow{X}\) permet un mouvement de translation, le long de cet axe, entre deux solides \(S_i\) et \(S_k\).
Nom | Liaison glissière |
|---|---|
Association de liaisons élémentaires | Appui plan + appui plan Pivot glissant + linéaire rectiligne... |
Degrés de mobilité liberté | 1 translation |
Schématisation |
|
Torseur cinématique associé | \(\left\{ \mathcal{V} \left( S_k / S_i \right)\right\}=\left\{ \begin{array}{c}\overrightarrow{\Omega} \left(S_k/S_i \right)=\overrightarrow{0}\\\overrightarrow{V} \left(A \in S_k/S_i \right)=V_x\cdot \overrightarrow{X}\end{array}\right\}_A=\left\{ \begin{array}{cc} 0 & V_x\\0 & 0 \\0 & 0\end{array}\right\}_{A,B}\) |
Validité de la forme canonique du torseur | Valable en tout point de l'espace |
Liaison hélicoïdale
Une liaison hélicoïdale d'axe \((O,\overrightarrow{X} )\) permet un mouvement de rotation autour de cet axe, et un mouvement de translation le long de cet axe entre deux solides \(S_i\) et \(S_k\).
Les mouvements de rotation et de translation sont liés par la relation \(V_x=\frac{p}{2\pi}.\omega_x\), p étant le pas de l'hélice.
Nom | Liaison hélicoïdale |
|---|---|
Surface de contact | hélicoïdales |
Degrés de mobilité liberté | 1 translation et 1 rotation liées |
Schématisation | |
Torseur cinématique associé | \(\left\{ \mathcal{V} \left( S_k / S_i \right)\right\}=\left\{ \begin{array}{c}\overrightarrow{\Omega} \left(S_k/S_i \right)=\omega_x\cdot \overrightarrow{X}\\\overrightarrow{V} \left(O \in S_k/S_i \right)=V_x\cdot \overrightarrow{X}\end{array}\right\}_O=\left\{ \begin{array}{cc} \omega_x & V_x\\0 & 0 \\0 & 0\end{array}\right\}_{O,B}\) |
Validité de la forme canonique du torseur | Valable en tout point de l'axe \((O,\overrightarrow{X})\) (donc en A) |
Liaison sphérique à doigt
Une liaison sphérique à doigt de centre \(O\) et de direction \(\overrightarrow{Y}\) permet deux mouvements de rotation entre deux solides \(S_i\) et \(S_k\).
Nom | Liaison sphérique à doigt |
|---|---|
Degrés de liberté | 2 rotations |
Schématisation | |
Torseur cinématique associé | \(\left\{ \mathcal{V} \left( S_k / S_i \right)\right\}=\left\{ \begin{array}{c}\overrightarrow{\Omega} \left(S_k/S_i \right)=\omega_x\cdot \overrightarrow{X}+\omega_z\cdot \overrightarrow{Z}\\\overrightarrow{V} \left(O \in S_k/S_i \right)=\overrightarrow{0}\end{array}\right\}_O=\left\{ \begin{array}{cc} \omega_x & 0\\0 & 0 \\\omega_z & 0\end{array}\right\}_{O,B}\) |
Validité de la forme canonique du torseur | Valable au point \(0\), centre des sphères |
Sa réalisation se fait essentiellement par une partie sphérique avec un ergot, montée dans une cavité sphérique rainurée. L'ergot se monte dans la rainure et son axe passe par le centre de la liaison.
Si l'axe \((O,\overrightarrow{Y})\) est dans le plan de la rainure et si l'axe \((O,\overrightarrow{X})\) est celui de l'ergot alors la rotation suivant l'axe \((O,\overrightarrow{Y})\) est bloquée.