Cas particulier de la modélisation plane
Intérêt de la modélisation plane
Généralement, la résolution analytique spatiale d'un problème de cinématique conduit à l'écriture de 6 équations scalaires. Mais dans le cas des problèmes plans (ou ramenés dans le plan), seules 3 équations scalaires sont nécessaires. Il est donc préférable de traiter dès le départ le problème dans le plan.
L'écriture des torseurs s'en trouve simplifiée ainsi que la résolution.
Méthode : Modélisation plane des liaisons normalisées
Dans l'écriture du torseur cinématique plan d'une liaison, seules subsistent, par rapport au torseur cinématique spatial :
la composante du vecteur rotation qui est perpendiculaire au plan ;
les deux composantes du vecteur vitesse qui sont contenues dans le plan.
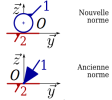
Exemple : liaison ponctuelle de normale \((O,\vec{z})\) modélisée dans le plan \((O,\vec{y},\vec{z} )\) :
Schéma cinématique plan | Torseur cinématique dans l'espace | Torseur cinématique dans le plan \((O,\vec{y},\vec{z})\) | |
Liaison ponctuelle (liaison sphère-plan) | \(\left\{ \begin{array}{cc} \omega_x &V_x\\\omega_y &V_y \\\omega_z &0\end{array}\right\}_{O,B}\) | \(\left\{ \begin{array}{cc} \omega_x & -\\- & V_y \\- & 0\end{array}\right\}_{O,B}\) |
Conditions permettant de ramener un problème spatial à un problème plan
Conditions liées à la structure du mécanisme
Le mécanisme admet un plan de symétrie.
Le mécanisme n'est animé que de mouvements plans parallèles.
Le mécanisme ne comprend que des liaisons dont les composantes des vitesses sont comprises dans le plan (ou dans des plans parallèles) et des rotations d'axes perpendiculaires au plan.
Il n'existe aucune translation de direction perpendiculaire au plan dans lequel on se ramène.
ATTENTION, ces conditions sont nécessaires mais pas toujours suffisantes.