Changer de base
Soient deux bases \(B_1\) et \(B_2\) de \(\mathcal{E}\) mobiles l'une par rapport à l'autre et \(\vec{V}\) un vecteur de \(\mathcal{E}\).
Soient les composantes de \(\vec{V}\) dans \(B_1\) :
Changer \(\overrightarrow{V}\) de base consiste à déterminer les composantes de \(\overrightarrow{V}\) dans \(B_2\) :
Le mouvement de \(B_2\) par rapport à \(B_1\) est caractérisé par trois rotations élémentaires. En SI, on décompose toujours les rotations en rotations élémentaires autour d'un vecteur de la base et on projette dans ces bases successives.
Exemple :
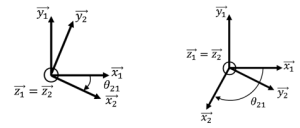
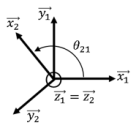
Exemple : \(B_2\) en rotation d'angle \(\theta_{21}\) autour de \(\overrightarrow{z_1}\) par rapport à \(B_1\). Cette définition est toujours traduite par une figure de projection telle que celles ci-dessous, où on commence par placer les repères comme sur la figure, puis l'axe de rotation, l'angle et enfin on complète les bases dans le sens direct.
Conseil : Remarque importante :
Deux points essentiels sont à respecter lors de la réalisation des figures de projection, pour limiter les risques d'erreur :
Les angles doivent être représentés dans le sens positif (cf. , « Orientation d'un angle par rapport à un vecteur »),
Les angles doivent être représentés avec une valeur appartenant à l'intervalle \([0;\frac{\pi}{2}]\)

Représentation possible quelle que soit la configuration du mécanisme dans le problème traité.
En utilisant la représentation conseillée, on obtient rapidement :
\(\overrightarrow{x_2}=\cos \theta_{21} \cdot \overrightarrow{x_1}+\sin \theta_{21} \cdot \overrightarrow{y_1}\)
\(\overrightarrow{y_2}=-\sin \theta_{21} \cdot \overrightarrow{x_1}+\cos \theta_{21} \cdot \overrightarrow{y_1}\)
\(\overrightarrow{x_1}=\cos \theta_{21} \cdot \overrightarrow{x_2}-\sin \theta_{21} \cdot \overrightarrow{y_2}\)
\(\overrightarrow{y_1}=\sin \theta_{21} \cdot \overrightarrow{x_2}+\cos \theta_{21} \cdot \overrightarrow{y_2}\)