Mouvements autorisés d'un solide par rapport à un autre solide
Deux solides \(S_i\) et \(S_k\) sont en contact lorsqu'une surface géométrique élémentaire liée à \(S_i\) s'appuie sur une surface géométrique élémentaire liée à \(S_k\). Les surfaces de contact géométriques élémentaires sont le plan, le cylindre de révolution et la sphère. Dans le cadre de ce cours, elles sont supposées indéformables.
Lorsqu'il existe une ou plusieurs surfaces de contact entre deux solides certains degrés de mobilités sont annulés par la liaison (au minimum 1 et au maximum 6).
Il est ainsi possible de répertorier un certain nombre de liaisons usuelles, autorisant certaines rotations et/ou certaines translations.
L'observation de la surface (ou des surfaces) de contact entre deux solides permet de proposer une liaison modélisant le comportement cinématique possible entre ces solides. Les liaisons élémentaires sont obtenues à partir du contact entre deux surfaces géométriques élémentaires (sphère, cylindre, plan).
Toutes les liaisons usuelles sont représentées graphiquement par un schéma normalisé qui seront présentés dans un tableau récapitulatif dans un document annexe.
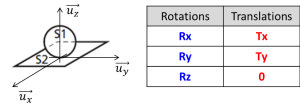
Définition : Contact entre une sphère et un plan
Ce type de contact entre deux solides est appelé liaison sphère plan (ou liaison ponctuelle). Elle possède 5 degrés de liberté (3 rotations + 2 translations).
Remarque importante : le respect de cette liaison impose le maintien du contact entre la sphère et le plan. C'est à dire que la translation selon z de la sphère par rapport au plan (Tz) est interdite dans les deux sens (selon \(+\vec{u_z}\) et selon \(-\vec{u_z}\)).
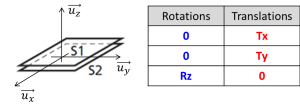
Définition : Contact entre deux plans
Ce type de contact entre deux solides est appelé liaison appui plan. Elle possède 3 degrés de liberté (1 rotation + 2 translations).
De nouveau, le respect de la liaison impose le maintien du contact entre les deux plans, la translation verticale est interdite vers le haut et vers le bas.
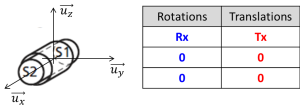
Définition : Contact entre deux cylindres
Ce type de contact entre deux solides est appelé liaison pivot glissant. Elle possède 2 degrés de liberté (1 rotation + 1 translation).
Définition : Contact entre deux sphères
Ce type de contact entre deux solides est appelé liaison sphérique ou liaison rotule. Elle possède 3 degrés de liberté (3 rotations).
Remarque : Liaisons composées
En plus de ces 4 liaisons élémentaires, il existe en construction mécanique plusieurs autres liaisons, obtenues par la combinaison des précédentes. Une norme défini certaines de ces liaisons (les plus couramment utilisées). Le but est de représenter des mouvements simples et fréquemment utilisés : les rotations et les translations.
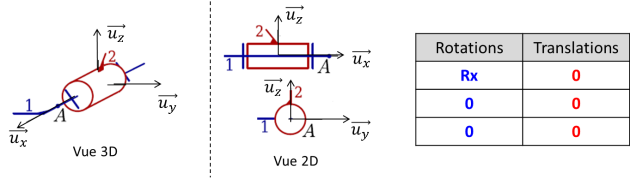
Définition : Liaison pivot
La liaison pivot permet de représenter un mouvement de rotation entre deux solides. Cette liaison possède un seul degré de liberté (1 rotation).
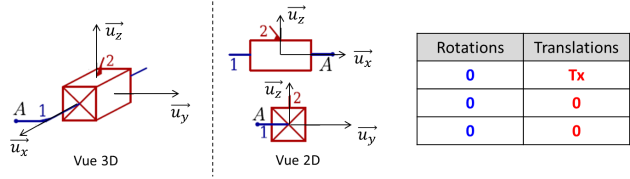
Définition : Liaison glissière
La liaison glissière permet de représenter un mouvement de translation entre deux solides. Cette liaison possède un seul degré de liberté (1 translation).
Exemple : Cas du manège à sensation
On remarque qu'à chaque liaison entre deux solides consécutifs, le mouvement est relativement simple et se décompose en quelques rotations ou translations bien déterminées :
la tige 6 du vérin est en translation par rapport au corps 5 du vérin. La direction de la translation \(\vec x_5\) ;
le bras 1 est en rotation par rapport au sol. L'axe de la rotation est \((O,\vec z_0)\).
mouvement du solide 1 par rapport au sol 0 : rotation d'axe \((O,\vec z_0)\) ;
mouvement du solide 2 par rapport au solide 1 : rotation d'axe \((C,\vec x_1)\) ;
mouvement du solide 3 par rapport au solide 2 : rotation d'axe \((D,\vec y_{22})\) ;
mouvement du solide 4 par rapport au solide 3 : rotation d'axe \((E,\vec x_3)\) ;
mouvement du solide 5 par rapport au sol : rotation d'axe \((A,\vec z_0)\) ;
mouvement du solide 6 par rapport au solide 5 : translation de direction \(\vec x_5\) ;
mouvement du solide 6 par rapport au solide 1 : rotation d'axe \((B,\vec z_0)\).
D'autres solides ont des mouvements plus complexes, comme le bras 4 par rapport au sol, qui combine rotations et translations.
Attention :
Pour un mouvement de rotation, il faut définir un axe de rotation (un point + un vecteur)
Pour un mouvement de translation, la direction de translation suffit (un vecteur).