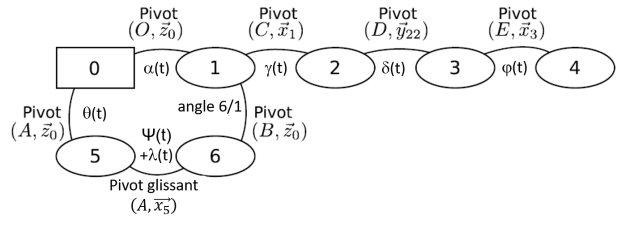
Cas du manège à sensations
On reprend l'exemple du manège dont le paramétrage complet est donné dans l'exercice précédent. Seul le graphe de liaison est rappelé ci-dessous.
Question
Exprimer les torseurs cinématiques suivants (le point d'expression sera choisi de façon judicieuse par vos soins). Précisez à quels types de torseurs particuliers correspondent ces torseurs.
\(\left\{\mathcal{V}\left(1/0\right)\right\}\)
\(\left\{\mathcal{V}\left(5/0\right)\right\}\)
\(\left\{\mathcal{V}\left(6/5\right)\right\}\)
Solution
Mouvement de 1 par rapport à 0 : rotation d'axe \((O,\vec{z_0})\). Le torseur sera écrit au point O (vitesse nulle car sur l'axe de rotation)
\(\left\{\mathcal{V}\left(1/0\right)\right\}=\left\{ \begin{array}{c}\overrightarrow{\Omega} \left(1/0 \right) \\\overrightarrow{V} \left(O \in 1/0 \right)\end{array}\right\}_O=\left\{ \begin{array}{c}\dot{\alpha}.\overrightarrow{z_0} \\\overrightarrow{0} \end{array}\right\}_O\)
Il s'agit d'un torseur glisseur, car \(\overrightarrow{\Omega}\left(1/0 \right).\overrightarrow{V} \left(O \in 1/0 \right)=0\)
Mouvement de 5 par rapport à 0 : rotation d'axe \((A,\vec{z_0})\). Le torseur sera écrit au point A (vitesse nulle car sur l'axe de rotation)
\(\left\{\mathcal{V}\left(5/0\right)\right\}=\left\{ \begin{array}{c}\overrightarrow{\Omega} \left(5/0 \right) \\\overrightarrow{V} \left(A \in 5/0 \right)\end{array}\right\}_A=\left\{ \begin{array}{c}\dot{\theta}.\overrightarrow{z_0} \\\overrightarrow{0} \end{array}\right\}_A\)
De même que précédemment, il s'agit d'un torseur glisseur.
Mouvement de 6 par rapport à 5 : liaison pivot glissant, donc translation dans la direction \(\vec{x_5}\) et rotation autour de l'axe \((A,\vec{x_5})\). Le torseur Le torseur sera écrit au point A ou au point B (vitesse nulle car sur l'axe de rotation).
\(\left\{\mathcal{V}\left( 6/5\right)\right\}=\left\{ \begin{array}{c}\overrightarrow{\Omega} \left(6/5 \right) \\\overrightarrow{V} \left(A \in 6/5 \right)\end{array}\right\}_B\)
Pour exprimer le vecteur vitesse de rotation de 5/6, il faut nommer l'angle correspondant (pas nommé dans le paramétrage initial). On le note \(\psi\).
\(\left\{\mathcal{V}\left(6/5\right)\right\}=\left\{ \begin{array}{c}\overrightarrow{\Omega} \left(6/5 \right) \\\overrightarrow{V} \left(A \in 6/5 \right)\end{array}\right\}_B=\left\{ \begin{array}{c} \dot{\psi}.\overrightarrow{x_5} \\\dot{\lambda}.\overrightarrow{x_5} \end{array}\right\}_B\)
Ce torseur ne correspond pas à une forme particulière (ni la résultante ni l'automoment ne sont nuls).
Question
Exprimer tous les torseurs précédents au point B
Solution
Mouvement de 1 par rapport à 0 :
\(\left\{\mathcal{V}\left(1/0\right)\right\}=\left\{ \begin{array}{c}\dot{\alpha}.\overrightarrow{z_0} \\\overrightarrow{0} \end{array}\right\}_O\)
Pour changer le torseur de point, il faut exprimer le vecteur vitesse au point B
\(\overrightarrow{V} \left( B \in 1/0 \right)=\overrightarrow{V} \left( O \in 1/0 \right)+\overrightarrow{BO}\wedge \overrightarrow{\Omega} \left(1/0\right)=\vec{0}-b.\vec{x_1}\wedge\dot{\alpha}.\vec{z_0}=b.\dot{\alpha}.\vec{y_1}\)
D'où :
\(\left\{\mathcal{V}\left(1/0\right)\right\}=\left\{ \begin{array}{c}\dot{\alpha}.\overrightarrow{z_0} \\b.\dot{\alpha}.\vec{y_1} \end{array}\right\}_B\)
Mouvement de 5 par rapport à 0 :
\(\left\{\mathcal{V}\left(5/0\right)\right\}=\left\{ \begin{array}{c}\dot{\theta}.\overrightarrow{z_0} \\\overrightarrow{0} \end{array}\right\}_A\)
De même que précédemment, il faut exprimer le vecteur vitesse au point B
\(\overrightarrow{V} \left( B \in 5/0 \right)=\overrightarrow{V} \left( A \in 5/0 \right)+\overrightarrow{BA}\wedge \overrightarrow{\Omega} \left(5/0\right)=\vec{0}-\lambda.\vec{x_5}\wedge\dot{\theta}.\vec{z_0}=-\lambda.\dot{\theta}.\vec{x_5}\wedge\vec{z_0}=\lambda.\dot{\theta}.\vec{y_5}\)
D'où :
\(\left\{\mathcal{V}\left(5/0\right)\right\}=\left\{ \begin{array}{c}\dot{\theta}.\overrightarrow{z_0} \\\lambda.\dot{\theta}.\vec{y_5}\end{array}\right\}_B\)
Mouvement de 6 par rapport à 5 :
\(\left\{\mathcal{V}\left(6/5\right)\right\}=\left\{ \begin{array}{c} \dot{\psi}.\overrightarrow{x_5} \\\dot{\lambda}.\overrightarrow{x_5} \end{array}\right\}_B\)
Le torseur est déjà exprimé au point B.
Question
A partir des résultats précédents, exprimer le torseur \(\left\{\mathcal{V}\left(6/1\right)\right\}\)
Solution
Par composition des vitesses :
\(\left\{\mathcal{V}\left(6/1\right)\right\}=\left\{\mathcal{V}\left(6/5\right)\right\}+\left\{\mathcal{V}\left(5/0\right)\right\}+\left\{\mathcal{V}\left(0/1\right)\right\}\)
Or, \(\left\{\mathcal{V}\left(0/1\right)\right\}=-\left\{\mathcal{V}\left(1/0\right)\right\}\)
Soit :
\(\left\{\mathcal{V}\left(6/1\right)\right\}=\left\{\mathcal{V}\left(6/5\right)\right\}+\left\{\mathcal{V}\left(5/0\right)\right\}-\left\{\mathcal{V}\left(1/0\right)\right\}\)
Les torseurs ayant tous été exprimés au point B, il est possible de les sommer directement en sommant les résultantes et les moments.
\(\left\{\mathcal{V}\left(6/1\right)\right\}=\left\{ \begin{array}{c} \dot{\psi}.\overrightarrow{x_5} \\\dot{\lambda}.\overrightarrow{x_5} \end{array}\right\}_B+\left\{ \begin{array}{c}\dot{\theta}.\overrightarrow{z_0} \\\lambda.\dot{\theta}.\vec{y_5}\end{array}\right\}_B-\left\{ \begin{array}{c}\dot{\alpha}.\overrightarrow{z_0} \\b.\dot{\alpha}.\vec{y_1} \end{array}\right\}_B=\left\{ \begin{array}{c}\dot{\psi}.\overrightarrow{x_5}+\left(\dot{\theta}-\dot{\alpha}\right).\overrightarrow{z_0} \\\dot{\lambda}.\overrightarrow{x_5}+\lambda.\dot{\theta}.\vec{y_5}-b.\dot{\alpha}.\vec{y_1} \end{array}\right\}_B\)