Cas d'un mouvement de rotation
Torseur cinématique dans le cas d'un mouvement de rotation

Pour décrire au mieux le déplacement d'un solide \(S_k\) en rotation par rapport à un repère \(R_i\), il suffit de choisir le repère \(R_k\) lié au solide \(S_k\) tel que l'un de ses axes (par exemple l'axe \((O_k,\vec{z}_k )\) soit confondu avec l'un des axes du repère \(R_i\) (par exemple l'axe \((O_i,\vec{z}_i )\) ET avec l'axe de rotation \((AB)\) tout au long du mouvement (cf. figure ci contre.). Le point \(O_k\) est choisi SUR l'axe de rotation \((AB)\).
Le paramètre décrivant le mouvement de la base\(B_k\) par rapport à la base \(B_i\) au cours du temps sera alors l'angle de rotation entre les deux bases. Cet angle est une fonction du temps.
Si un solide S\(_k\) est animé d'un mouvement de rotation par rapport au repère \(R_i\), alors le vecteur-vitesse du point A, appartenant au solide \(S_k\), par rapport au repère \(R_i\) s'écrit, d'après la relation de changement de point : \(\overrightarrow{V} (A \in k/i)=\overrightarrow{V}(O_k \in k/i)+\overrightarrow{AO_k }∧\overrightarrow{\Omega}(k/i)\).
Or \(\overrightarrow{V}(O_k \in k/i)=\overrightarrow{0}\) puisque le point \(O_k\) appartient à l'axe de rotation. Donc le champ des vecteurs-vitesse pour un solide en rotation autour d'un axe fixe s'écrit : \(\overrightarrow{V} (A \in k/i)=\overrightarrow{AO_k }∧\overrightarrow{\Omega}(k/i)\).
Le torseur cinématique caractérisant le mouvement de \(S_k\) par rapport à \(R_i\) a alors la forme suivante :
Ce torseur est un torseur glisseur
Propriété 1 :
Quel que soit le point \(M_1\) appartenant au solide \(S_k\) pour lequel on cherche à déterminer le vecteur-vitesse \(\overrightarrow{V}(M_1\in k/i)\), il existe un point \(H_{M_1}\), projection orthogonale de \(M_1\) sur l'axe de rotation \(\Delta\). On a alors la relation suivante :
\(\overrightarrow{V}(M_1\in k/i)=\overrightarrow{M_1 H_{M_1}}\wedge\overrightarrow{\Omega}(k/i)\) avec \(\overrightarrow{\Omega}(k/i)\perp\overrightarrow{M_1 H_{M_1}}\).
La norme du-vecteur vitesse \(\overrightarrow{V}(M_1\in k/i)\) est donc égale à : \(\left\|\overrightarrow{V}(M_1\in k/i)\right\|=\left\|\overrightarrow{M_1 H_{M_1}}\right\|\cdot\left\|\overrightarrow{\Omega}(k/i)\right\|\)
On pose :
\(R_1=\left\|\overrightarrow{M_1 H_{M_1}}\right\|\), distance du point \(M_1\) à l'axe de rotation \(\Delta\) ;
\(\omega=\dot{\theta}=\left\|\overrightarrow{\Omega}(k/i)\right\|\), avec \(\omega\) la norme de la vitesse de rotation du solide \(S_k\) par rapport au repère \(R_i\) et \(\theta\) l'angle de rotation du solide \(S_k\) par rapport au repère \(R_i\).
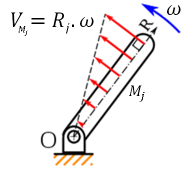
\(\left\|\overrightarrow{V}(M_1\in k/i)\right\|=R_1\cdot \omega=R_1\cdot \dot{\theta}\)
On peut en déduire que la norme du vecteur-vitesse d'un point \(M_j\), appartenant à un solide \(S_k\) en rotation par rapport à un repère \(R_i\), est proportionnelle à la distance du point \(M_j\) à l'axe de rotation \((\Delta)\).
On peut en déduire que :
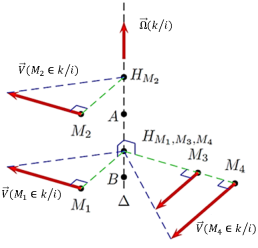
tous les points situés à une même distance de l'axe de rotation (∆) ont des vecteurs-vitesse de même norme (cas des points \(M_1\), \(M_2\) et \(M_3\) sur la figure : propriétés particulières du champ des vecteurs vitesse du solide Sk en rotation par rapport au repère Ri autour de l'axe ∆[1]).
tous les points situés sur une même génératrice parallèle à l'axe de rotation ont des vecteurs-vitesse de même direction, même sens et même norme (cas des points \(M_1\) et \(M_2\) sur la figure : propriétés particulières du champ des vecteurs vitesse du solide Sk en rotation par rapport au repère Ri autour de l'axe ∆[2]).