Engrenages coniques
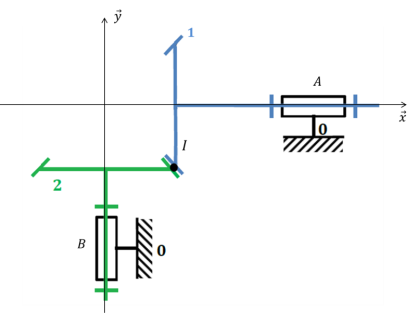
Hypothèse : les axes des deux roues sont concourants et perpendiculaires. On pose \(\overrightarrow{BI}=d.\cdot\vec{y}+R_2\cdot\vec{x}\) et \(\overrightarrow{AI}=-l\cdot\vec{x}-R_1\cdot\vec{y}\).
Sur le même raisonnement en exprimant le RGS en I :\(\overrightarrow{V}\left(I \in 2/0\right)-\overrightarrow{V}\left(I \in 1/0\right)=\overrightarrow{0}\)
Or :
\(\overrightarrow{V}\left(I \in 1/0\right)=\overrightarrow{IA}\wedge\overrightarrow{\Omega}_{1/0}=\left(l\cdot\vec{x}+R_1\cdot\vec{y}\right)\wedge\omega_{10}\cdot\vec{x}=-R_1 \cdot \omega_{10} \cdot\vec{z}\)
\(\overrightarrow{V}\left(I \in 2/0\right)=\overrightarrow{IB}\wedge\overrightarrow{\Omega}_{2/0}=\left(-d.\cdot\vec{y}-R_2\cdot\vec{x}\right)\wedge\omega_{20}\cdot\vec{y}=-R_2 \cdot \omega_{20} \cdot\vec{z}\)
D'où la relation \(R_1 \cdot \omega_{10} -R_2 \cdot \omega_{20} =0\) et on en déduit le rapport de transmission :
Remarque : de nouveau, le signe du rapport de réduction dépend du paramétrage du problème.