Engrenage simple à denture droite extérieure
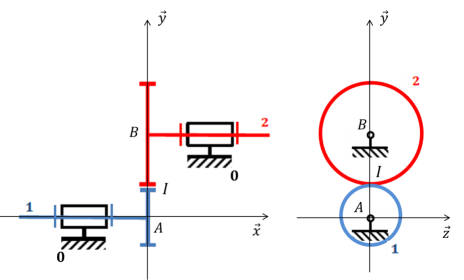
Question
Donner l'expression des torseurs cinématiques \(\left\{\mathcal{V}_{1/0}\right\}\) et \(\left\{\mathcal{V}_{2/0}\right\}\) :
Solution
\(\left\{\mathcal{V}_{1/0}\right\}=\left\{ \begin{array}{c}\omega_{10}\cdot \overrightarrow{x} \\ \overrightarrow{0} \end{array}\right\}_A\)
\(\left\{\mathcal{V}_{2/0}\right\}=\left\{ \begin{array}{c}\omega_{20}\cdot \overrightarrow{x} \\ \overrightarrow{0} \end{array}\right\}_B\)
Question
Écrire la condition de roulement sans glissement en I :
Solution
\(\overrightarrow{V}\left(I \in 2/1\right)=\overrightarrow{0}\)
Question
En déduire la relation entre \(\omega_{10}\) et \(\omega_{20}\).
Solution
\(\overrightarrow{V}\left(I \in 2/1\right)=\overrightarrow{0}=\overrightarrow{V}\left(I \in 2/0\right)-\overrightarrow{V}\left(I \in 1/0\right)\)
Il faut déplacer les deux vitesses au point I :
\(\overrightarrow{V}\left(I \in 1/0\right)=\overrightarrow{IA}\wedge\overrightarrow{\Omega}_{1/0}=R_1 \cdot \omega_{10} \cdot\vec{z}\)
\(\overrightarrow{V}\left(I \in 2/0\right)=\overrightarrow{IB}\wedge\overrightarrow{\Omega}_{2/0}=-R_2 \cdot \omega_{20} \cdot\vec{z}\)
On en déduit :
\(R_1 \cdot \omega_{10} \cdot\vec{z}+R_2 \cdot \omega_{20} \cdot\vec{z}=\overrightarrow{0}\)
Et donc :