Caractéristiques de l'engrenage cylindrique
Condition d'engrènement
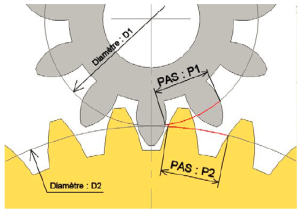
Pour assurer l'engrènement on doit faire en sorte que les dents d'une roue s'intercalent bien entre les dents de l'autre roue ; pour cela, il faut introduire la notion de « PAS » de la denture (voir la figure ci-contre).
Le « PAS » doit être identique sur chacune des deux roues : P1=P2.
Diamètre primitif et Module
On appelle cercles primitifs, ou cylindres primitifs, le contour de roues cylindriques qui remplaceraient les roues dentées, en transmettant le mouvement sans glissement, de la même façon que l'engrenage; on appelle diamètres primitifs les diamètres de ces roues cylindriques fictives.
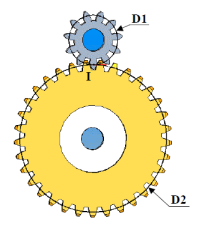
Soit \(D_1\) le diamètre primitif de la roue 1 ;
Soit \(D_2\) le diamètre primitif de la roue 2 ;
Soit \(Z_1\) le nombre de dents de la roue 1 ;
Soit \(Z_2\) le nombre de dents de la roue 2 ;
Le pas s'exprime en fonction de la circonférence et du nombre de dent sur chaque roue :
\(P_1=\frac{\pi D_1}{Z_1}\) ; \(P_2=\frac{\pi D_2}{Z_2}\)
Et lorsqu'on exprime la relation \(P_1=P_2\),on obtient∶\(\frac{D_1}{Z_1} =\frac{D_2}{Z_2}\)
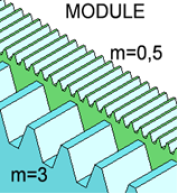
Ce rapport \(\frac{D}{Z}\) est appelé module de la denture.
On retiendra que pour que deux roues dentées puissent engrener l'une avec l'autre il est nécessaire qu'elles aient le même module.
\(D=m\cdot Z\)
\(P=\pi\cdot m\)
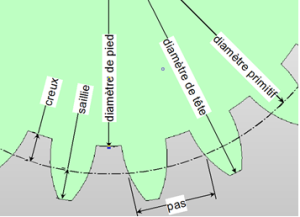
A titre informatif, d'autres diamètres que le diamètre primitif sont définis sur une roue dentée, comme par exemple le « diamètre de pied » (diamètre au fond des dents) ou le « diamètre de tête » (diamètre en haut des dents). Les relations entre ces différents diamètres sont normalisées, mais le programme de CPGE ne porte pas sur l'étude détaillée de la géométrie des engrenages.