Engrenage simple à denture droite intérieure
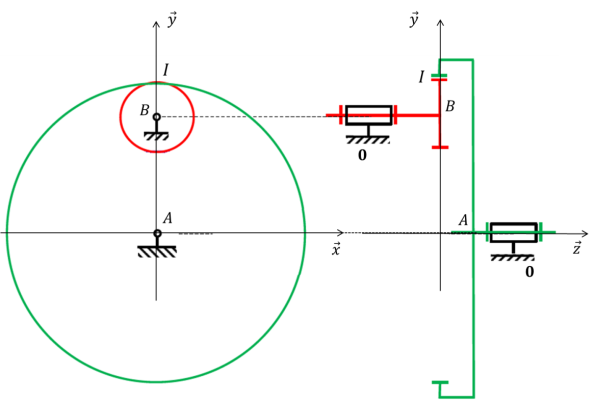
Selon le même raisonnement :\(\overrightarrow{V}\left(I \in 2/0\right)-\overrightarrow{V}\left(I \in 1/0\right)=\overrightarrow{0}\)
Or :
\(\overrightarrow{V}\left(I \in 1/0\right)=\overrightarrow{IA}\wedge\overrightarrow{\Omega}_{1/0}=R_1 \cdot \omega_{10} \cdot\vec{z}\)
\(\overrightarrow{V}\left(I \in 2/0\right)=\overrightarrow{IB}\wedge\overrightarrow{\Omega}_{2/0}=R_2 \cdot \omega_{20} \cdot\vec{z}\)
D'où la relation \(R_1 \cdot \omega_{10} -R_2 \cdot \omega_{20} =0\) et on en déduit le rapport de transmission :
\[r=\frac{\omega_{20}}{\omega_{10}}=\frac{R_1}{R_2}=\frac{Z_1}{Z_2}\]