Réponse à une rampe non unitaire
La méthode poursuivie est la même que pour la réponse à un échelon ou un dirac : écriture de \(e(t)\) en temporel, passage dans le domaine de Laplace, calcul de la sortie en Laplace puis, après décomposition en éléments simples, retour en temporel.
L'entrée sous forme de rampe unitaire s'écrit : \(e(t)=e_0.t.u(t)\), d'où \(E(p)=e_0/p^2\).
La sortie, dans le domaine de Laplace, vaut donc :
\(S(p)=\frac{e_0}{p^2}\cdot \frac{K}{1+\tau\cdot p}\)
On peut donc proposer la décomposition en éléments simples suivante : \(S(p)=\frac{\alpha}{p}+\frac{\beta}{p^2} +\frac{\gamma}{1+\tau.p}\)
D'où, toujours par identification : \(S(p)=K.e_0.\left[ \frac{1}{p^2}-\frac{\tau}{p} +\frac{\tau^2}{1+\tau.p}\right]\)
La transformée inverse de Laplace est alors la suivante : \(s(t)=K \cdot e_0 \cdot [ t-\tau+\tau \cdot e^{-t/\tau} ] \cdot u(t)\)
Fondamental : réponse à une rampe
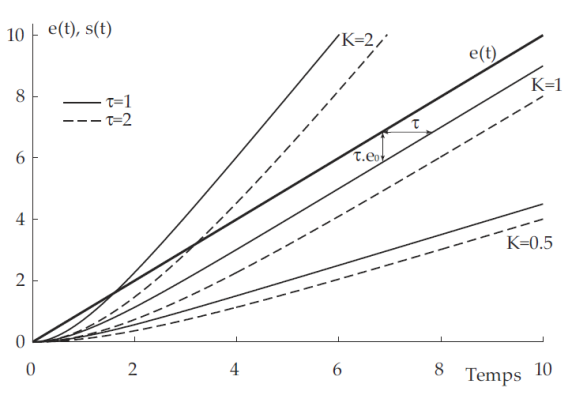
Cette réponse est tracée sur la figure ci-dessus et présente les propriétés suivantes :
La valeur à l'origine est nulle
La pente à l'origine est nulle
L'asymptote quand \(t\to\infty\) vaut \(K.e_0.(t-\tau)\) et cette asymptote coupe l'axe des abscisses en \(t=\tau\)
Dans le cas particulier où \(K=1\), l'asymptote est parallèle à la consigne et il est alors possible de définir une erreur en vitesse (ou encore erreur de trainée ou erreur de poursuite) entre la consigne et la réponse. Cette erreur de vitesse vaut \(\tau.e_0\).