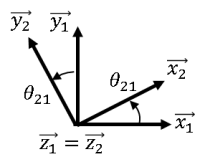
Soit la figure de changement de base ci-joint,
Question
Calculer en utilisant la formule de Bour, les dérivées suivantes :
\(\left.\frac{d\overrightarrow{x_2}}{dt}\right|_{B_1}\)
\(\left.\frac{d\overrightarrow{y_1}}{dt}\right|_{B_2}\)
Solution
\(\left.\frac{d\overrightarrow{x_2}}{dt}\right|_{B_1}=\left.\frac{d\overrightarrow{x_2}}{dt}\right|_{B_2}+\overrightarrow{\Omega}(2/1)\wedge \overrightarrow{x_2}=\dot{\theta}_{21}\cdot \overrightarrow{z_2}\wedge \overrightarrow{x_2}=\dot{\theta}_{21}\cdot \overrightarrow{y_2}\)
\(\left.\frac{d\vec{y_1}}{dt}\right|_{B_2}=\left.\frac{d\overrightarrow{y_1}}{dt}\right|_{B_1}+\overrightarrow{\Omega}(1/2)\wedge \overrightarrow{y_1}=-\dot{\theta}_{21}\cdot \overrightarrow{z_1}\wedge \overrightarrow{y_1}=\dot{\theta}_{21}\cdot \overrightarrow{x_1}\)