Question
Avec la figure de changement de base ci-joint, calculer les produits vectoriels ci-dessous :
\(\vec{x_1}\wedge\vec{x_1}\)
\(\vec{x_1}\wedge\vec{y_1}\)
\(\vec{x_1}\wedge\vec{z_1}\)
\(\vec{x_1}\wedge\vec{x_2}\)
\(\vec{x_1}\wedge\vec{y_2}\)
\(\vec{x_1}\wedge\vec{z_2}\)
\(\vec{y_1}\wedge\vec{x_2}\)
\(\vec{y_2}\wedge\vec{y_1}\)
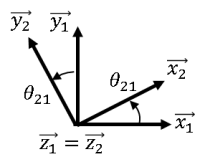
Solution
\(\vec{x_1}\wedge\vec{x_1}={\vec0}\)
\(\vec{x_1}\wedge\vec{y_1}=\vec{z_1}\)
\(\vec{x_1}\wedge\vec{z_1}=-\vec{y_1}\)
\(\vec{x_1}\wedge\vec{x_2}=sin\theta_{21}.\vec{z_1}\)
\(\vec{x_1}\wedge\vec{y_2}=sin(\frac{\pi}{2}+\theta_{21}).\vec{z_1}=cos\theta_{21}.\vec{z_1}\)
\(\vec{x_1}\wedge\vec{z_2}=\vec{x_1}\wedge\vec{z_1}=-\vec{y_1}\)
\(\vec{y_1}\wedge\vec{x_2}=-sin(\frac{\pi}{2}-\theta_{21}).\vec{z_1}=-cos\theta_{21}.\vec{z_1}\)
\(\vec{y_2}\wedge\vec{y_1}=-sin(\theta_{21}).\vec{z_1}\)