Vecteur vitesse de rotation d'une base Bk par rapport à une base Bi
Ce vecteur est utilisé pour représenter la vitesse de rotation de deux bases l'un par rapport à l'autre. On note :
\(\overrightarrow{ \Omega } \left(B_k/B_i \right)\) le vecteur vitesse de rotation de la base \(B_k\) par rapport à la base \(B_i\),
\(\overrightarrow{ \Omega } \left(B_i/B_k \right)\) le vecteur vitesse de rotation de la base \(B_i\) par rapport à la base\(B_k\).
Ce vecteur est défini par :
sa direction, qui est parallèle à l'axe de rotation des deux repères l'un par rapport à l'autre,
sa norme, qui est égale à la vitesse de rotation (en rad.s-1), c'est-à-dire à la dérivée de l'angle (en rad) paramétrant la position des deux repères,
son sens, qui doit être soigneusement défini par rapport à l'axe de rotation.
Exemple :
soit deux bases \(B_2(\overrightarrow{x_2},\overrightarrow{y_2},\overrightarrow{z_2})\) et \(B_1(\overrightarrow{x_1},\overrightarrow{y_1},\overrightarrow{z_1})\), avec \(B_2\) en rotation d'angle \(\theta_{21}\) autour de \(\overrightarrow{z_1}=\overrightarrow{z_2}\) par rapport à \(B_1\) selon la figure ci-contre.
On voit que l'angle \(\theta_{21}\) est orienté de 1 vers 2 (de \(\overrightarrow{x_1}\) vers \(\overrightarrow{x_2}\) et de \(\overrightarrow{y_1}\) vers \(\overrightarrow{y_2}\), il est donc bien représentatif de la rotation de la base 2 par rapport à la base 1.
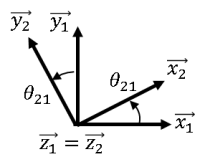
On peut alors définir le vecteur vitesse de rotation de R_2 par rapport à R_1 :
Si on souhaite définir le vecteur vitesse de rotation de \(B_1\) par rapport à \(B_2\), la direction est identique et l'angle relatif entre les deux repères est le même, mais il sera cette fois orienté de 2 vers 1 (donc compté négativement). D'où :