Fonction de transfert du second ordre en régime pseudo-périodique.
Pour \(\xi<1\), à partir de : \(H(p)=\frac{K}{\left(1+ \dfrac{2\xi}{\omega_0} p+\dfrac{p^2}{\omega_0^2}\right)}\), on écrit :
\(H(j\omega)=\frac{K}{\left(1+j\dfrac{2\xi\omega}{\omega_{0}}-\dfrac{\omega^2}{\omega_{0}^2}\right)}\)
Gain en dB | \(\left|H(j\omega)\right|_{dB}=20\log K+20\log\dfrac{1}{\left(\sqrt{\left(1-\frac{\omega^2}{\omega_{0}^2}\right)^2+\left(\frac{2\xi\omega}{\omega_{0}}\right)^2}\right)}\) |
Phase \(\omega<\omega_0\) | \(\arg\left(H(j\omega)\right)=-\arctan\left(\dfrac{2\xi\omega\omega_0}{\omega_0^2-\omega^2}\right)\) |
Phase \(\omega=\omega_0\) | \(\arg\left(H(j\omega_0)\right)=-90°\) |
Phase \(\omega>\omega_0\) | \(\arg\left(H(j\omega)\right)=-\pi+\arctan\left(\dfrac{2\xi\omega\omega_0}{\omega_0^2-\omega^2}\right)\) |
Tracé asymptotique du diagramme de Bode
Si \(\omega \to 0\) alors \(\left\lbrace\begin{array}{l}\left|H(\omega)\right|\approx K \\ \\ \varphi(\omega)\approx 0°\\\end{array}\right.\) donc \(\left\lbrace\begin{array}{l}\left|H(\omega)\right|_{dB}\approx 20\log K \\ \\ \varphi(\omega)\approx 0° \\\end{array}\right.\)
Si \(\omega \to \infty\) alors \(\left\lbrace\begin{array}{l}\left|H(\omega)\right|\approx \frac{K\cdot \omega_0^2}{\omega^2} \\ \\ \varphi(\omega)\approx -180°\\\end{array}\right.\) donc \(\left\lbrace\begin{array}{l}\left|H(\omega)\right|_{dB}\approx 20\log \frac{K}{\omega_0^2}-40\log{\omega} \\ \\ \varphi(\omega)\approx -180° \\\end{array}\right.\)
La courbe de gain en décibels du diagramme de Bode d'un système du second ordre présente une asymptote horizontale à 20.logK lorsque la pulsation est faible et une asymptote oblique de -40 dB par décade de pente (décade : intervalle[ω;10.ω]) lorsque la pulsation est élevée.
Démonstration : \(\left|H(10.\omega)\right|_{dB}\approx 20\log \frac{K}{\omega_0^2}-40\log{10.\omega}= 20\log \frac{K}{\omega_0^2}-40\log 10 -40\log{\omega}\)
donc \(\left|H(10.\omega)\right|_{dB}=20\log \frac{K}{\omega_0^2}-40 -40\log{\omega}=\left|H(\omega)\right|_{dB}-40 dB\)
La courbe de phase du diagramme de Bode d'un système du second ordre présente une asymptote horizontale à 0° lorsque la pulsation est faible et une asymptote horizontale à -180° lorsque la pulsation est importante.
Les deux asymptotes de la courbe de gain en décibels se croisent en un point dont l'abscisse est \(\omega_0\) la pulsation propre.
Fondamental : Tracé asymptotique et réel
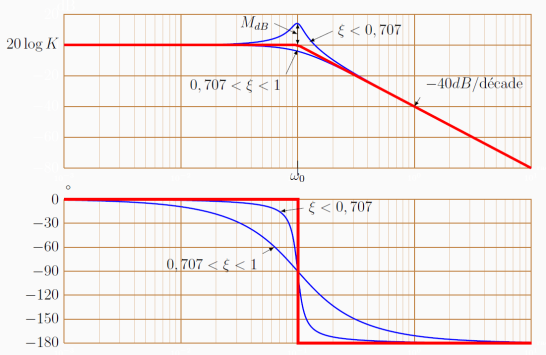
Remarque : Résonance
Il y a résonance pour \(\xi<\dfrac{\sqrt{2}}{2}\)
Lorsqu'il y a résonance, la courbe de gain possède une valeur maximale qui peut être déterminée à l'aide du facteur de surtension en dB :
\(M_{dB}=20 \log \dfrac{1}{2.\xi\sqrt{1-\xi^2}}\)
Cette valeur maximale se trouve à la pulsation de résonance : \(\omega_r=\omega_0\sqrt{1-2\xi^2}\)
(La démonstration n'est pas donnée dans ce cours mais consiste juste à chercher le maximum à l'aide d'une dérivée de l'expression du gain).
Méthode : Tracer du diagramme de Bode d'un second ordre
Identifier K et calculer \(20\log K\).
Identifier \(\omega_0\).
Pour le gain : tracer une asymptote horizontale de gain \(20 \log K\) jusqu'à la pulsation \(\omega_0\) puis tracer une asymptote ayant une pente de -40dB par décade.
Identifier \(\xi\).
Vérifier si \(\xi<0,707\), dans ce cas calculer la pulsation de résonance \(\omega_r\) et le facteur de surtension en dB \(M_{dB}\).
Tracer une courbe réelle en faisant apparaître la valeur de résonance à \(20 \log K +M_{dB}\).
Pour la phase : tracer une asymptote horizontale à 0° jusqu'à la pulsation \(\omega_0\) puis tracer une asymptote horizontale à -180°.
La courbe réelle de phase varie en fonction de \(\xi\).
Méthode : Identifier un second ordre sous amorti à partir de son diagramme de Bode
Vérifier sur la courbe de gain la pente est de -40dB/décade et que la phase tend vers -180° pour \(\omega\) tendant vers \(+\infty\).
Relever la valeur du gain \(20 \log K\) pour \(\omega\) tendant vers 0 et en déduire K.
Trouver l'intersection entre les deux asymptotes de gain, relever \(\omega_0\) . Autre solution, relever \(\omega_0\) correspondant à une phase de -90°.
L'identification de \(\xi\) n'est vraiment évidente que s'il y a une résonance. En effet, dans ce cas il suffit de relever \(M_{dB}\) et de calculer \(\xi\).
