Fonction de transfert du second ordre en régime critique.
Fondamental :
pour \(\xi=1\), à partir de : \(H(p)=\frac{K}{\left(1+ \tau p\right)^2}\), on écrit :
\(H(j\omega)=\frac{K}{\left(1+ j\tau \omega\right)^2}=\frac{K}{\left(1+j\frac{\omega}{\omega_0}\right)^2}\)
On en déduit :
Gain en dB | \(\left|H(j\omega)\right|_{dB}=20 \log K+2\times 20.\log\dfrac{1}{\left(\sqrt{1+\frac{\omega^2}{\omega_0^2}}\right)}\) |
Phase | \(arg\left(H(j\omega)\right)=-2\times\arctan\left(\frac{\omega}{\omega_0}\right)\) |
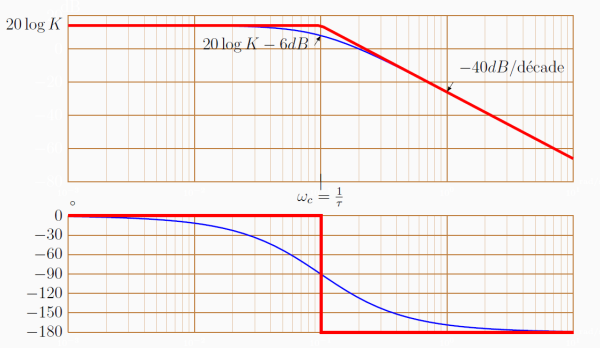
Méthode : Tracer du diagramme de Bode
On peut remarquer que le tracé de ce diagramme de Bode est le résultat de la multiplication par 2 du tracé d'une fonction de transfert du premier ordre.
La pente de la courbe de gain est multipliée par 2 : -40dB/décade.
La courbe réelle passe à -\(3dB \times 2=-6dB\) sous la cassure des asymptotes.
La phase est aussi multipliée par 2 : \(-180° \leq \arg(H(p)) \leq 0\).