Fonction de transfert du second ordre en régime apériodique.
Fondamental :
Pour \(\xi>1\), à partir de : \(H(p)=\frac{K}{\left(1+ \tau_1 p\right)\left(1+ \tau_2 p\right)}\) on écrit :
\(H(j\omega)=\frac{K}{\left(1+ j\tau_1 \omega\right)\left(1+ j\tau_2 \omega\right)}=\frac{K}{\left(1+j\frac{\omega}{\omega_{1}}\right)\left(1+j\frac{\omega}{\omega_{2}}\right)}\)
On en déduit :
On pose \(H_1(p)=\dfrac{1}{1+\dfrac{p}{\omega_1}}\) et \(H_2(p)=\dfrac{1}{1+\dfrac{p}{\omega_2}}\).
Gain en dB | \(\left|H(j\omega)\right|_{dB}=20 \log K+\left|H_1(j\omega)\right|_{dB}+\left|H_2(j\omega)\right|_{dB}\) |
Phase | \(arg\left(H(j\omega)\right)=arg\left(H_1(j\omega)\right)+arg\left(H_2(j\omega)\right)\) |
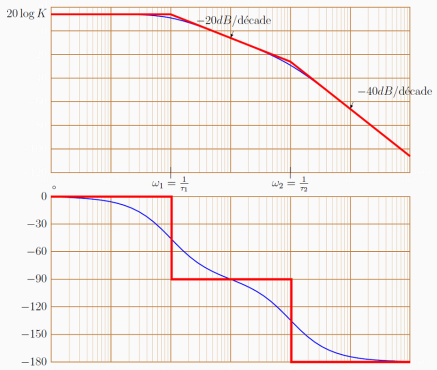
Méthode : Tracer du diagramme de Bode
On peut remarquer que le tracé de ce diagramme de Bode est le résultat de l'addition des tracés de deux fonctions de transfert du premier ordre.

Le diagramme de Bode asymptotique d'un système du second ordre fortement amorti (ξ>1) est constitué de 3 asymptotes pour la courbe de gain en décibels et de 3 asymptotes pour la courbe de phase.
Le diagramme de Bode réel en gain en décibels est proche du diagramme asymptotique (échelle logarithmique) et il passe 3 dB en dessous des asymptotes à chaque point de cassure si les deux pulsations de cassures \(\omega_1\) et \(\omega_2\) sont suffisamment éloignées (au moins une décade).
Le diagramme de Bode réel en phase est relativement éloigné des asymptotes (cf. premier ordre).