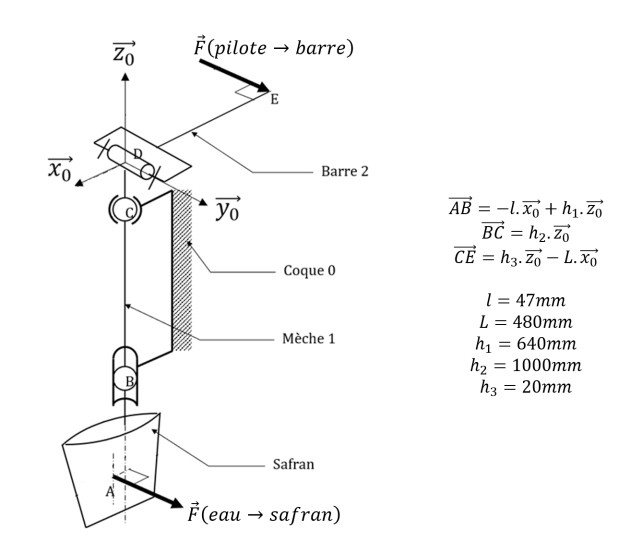
L'étude porte sur l'ensemble safran, mèche, barre, schématisé ci-dessous. La force hydrodynamique sur le safran a été déterminée précédemment, elle est notée \(\overrightarrow{F}(\text{eau} \rightarrow \text{safran})\). Il est important de déterminer l'effort \(\overrightarrow{F}(\text{pilote} \rightarrow \text{barre})\) que doit fournir le pilote automatique pour pouvoir dimensionner son vérin. Le poids des différentes pièces est négligé, et les liaisons sont considérées comme parfaites.

On considère que les efforts \(\overrightarrow{F}(\text{pilote} \rightarrow \text{barre})\) et \(\overrightarrow{F}(\text{eau} \rightarrow \text{safran})\) sont portés par l'axe \(\overrightarrow{y_0}\).

Question

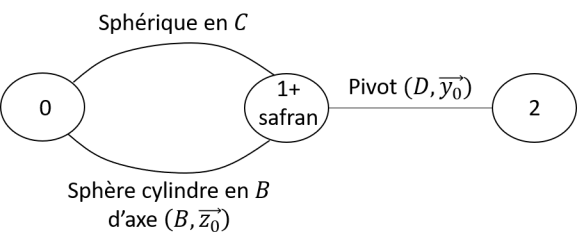
Tracer le graphe des liaisons structurel.

Solution

Question

Donner les torseurs des actions mécaniques transmissibles des deux liaisons parfaites entre les solides 0 et 1

Solution

\[\left\{ \mathcal{T} \left(0\rightarrow 1\right)\right\}_C =\left\{ \begin{array}{cc} X_{01C} & 0\\ Y_{01C} & 0 \\ Z_{01C} & 0 \end{array}\right\}_{C,\left(\vec{x_0},\vec{y_0},\vec{z_0}\right)}\] et \[\left\{ \mathcal{T} \left(0\rightarrow 1\right)\right\}_B =\left\{ \begin{array}{cc} X_{01B} & 0\\ Y_{01B} & 0 \\ 0 & 0 \end{array}\right\}_{B,\left(\vec{x_0},\vec{y_0},\vec{z_0}\right)}\]

Question

Exprimer le torseur des actions mécaniques transmissibles équivalent entre les solides 0 et 1. A quelle liaison correspond ce torseur ?

Solution

Les liaisons sont en parallèles, le torseur équivalent est égal à la somme des deux torseurs précédemment exprimés. Attention, il faut que les deux torseurs soient écrits au même point pour pouvoir les sommer (en C) :

\(\begin{align*}\overrightarrow{\mathcal{M}}(C,0 \rightarrow 1)_B&=\overrightarrow{\mathcal{M}}(B,0 \rightarrow 1)_B+\overrightarrow{CB} \wedge \vec{F}(0 \rightarrow 1)\\&=\overrightarrow{0}-h_2.\overrightarrow{z_0} \wedge (X_{\text{01B}}.\overrightarrow{x_0}+Y_{\text{01B}}.\overrightarrow{y_0})\\&=-h_2.X_{\text{01B}}.\overrightarrow{y_0}+h_2.Y_{\text{01B}}.\overrightarrow{x_0}\end{align*}\)

D'où le torseur équivalent :

\[\left\{ \mathcal{T} \left(0\rightarrow 1\right)\right\}_{eq} =\left\{ \begin{array}{cc} X_{01C} & 0\\ Y_{01C} & 0 \\ Z_{01C} & 0 \end{array}\right\}_{C,\left(\vec{x_0},\vec{y_0},\vec{z_0}\right)} +\left\{ \begin{array}{cc} X_{01B} & h_2*Y_{01B}\\ Y_{01B} & -h_2*X_{01B} \\ Z_{01B} & 0 \end{array}\right\}_{C,\left(\vec{x_0},\vec{y_0},\vec{z_0}\right)} \]
\[\left\{ \mathcal{T} \left(0\rightarrow 1\right)\right\}_{eq} =\left\{ \begin{array}{cc} X_{01C}+X_{01B} & h_2*Y_{01B}\\ Y_{01C}+Y_{01B} & -h_2*X_{01B} \\ Z_{01C}+Z_{01B} & 0 \end{array}\right\}_{C,\left(\vec{x_0},\vec{y_0},\vec{z_0}\right)}\]

On reconnaît le torseur d'actions mécaniques transmissibles d'une liaison pivot d'axe \((C,\vec{z_0})\)

Question

Tracer le nouveau graphe des liaisons fonctionnel, en utilisant la liaison équivalente déterminée précédemment

Solution

Graphe de liaison (avec actions mécaniques extérieures)

On cherche à déterminer l'expression de l'effort \(\overrightarrow{F}(\text{pilote} \rightarrow \text{barre})\) que doit fournir le pilote automatique en fonction de la force hydrodynamique appliquée sur le safran  \(\overrightarrow{F}(\text{eau} \rightarrow \text{safran})\) .

Question

Proposer le système à isoler répondre à la problématique posée.

Solution

On isole l'ensemble {1+safran+2} pour ne pas "couper" d'autre liaison que la liaison pivot entre le bati 0 et l'ensemble bras de mèche 1 + safran.

Question

Faire le bilan des actions mécanique extérieures appliquées sur le système isolé (écrire tous les torseurs modélisant ces actions mécaniques).

Solution

  • Action mécanique de la liaison pivot 0 sur 1 : \(\left\{\mathcal{T}({0} \rightarrow {1})\right\}=\left\{ \begin{array}{cc}X_{01} & L_{01}\\Y_{01} & M_{01} \\Z_{01} & 0\end{array}\right\}_{C,\left(\vec{x_0},\vec{y_0},\vec{z_0}\right)}\) (ce torseur est identique en tout point de l'axe \((C,\vec{z_0})\), donc en B ; C et D).

  • Action mécanique du pilote sur la barre : \(\left\{\mathcal{T}({pilote} \rightarrow {barre})\right\}=\left\{ \begin{array}{c}\overrightarrow{F} \left({pilote} \rightarrow {barre} \right) \\\overrightarrow{0}\end{array}\right\}_E\)

  • Action mécanique de l'eau sur le safran : \(\left\{\mathcal{T}({eau} \rightarrow {safran})\right\}=\left\{ \begin{array}{c}\overrightarrow{F} \left({eau} \rightarrow {safran} \right) \\\overrightarrow{0}\end{array}\right\}_A\)

Question

Écrire toutes les équations d'équilibre du système isolé.

Solution

On exprime tous les torseurs au point C (pour ne pas changer de point le torseur de la liaison pivot) :

\(\begin{align*}\overrightarrow{\mathcal{M}}(C,{pilote} \rightarrow {barre})&=\overrightarrow{\mathcal{M}}(E,{pilote} \rightarrow {barre})+\overrightarrow{CE} \wedge \vec{F}({pilote} \rightarrow {barre})\\&=\overrightarrow{0}+(h_{3}.\overrightarrow{z_0}-L.\overrightarrow{x_0}) \wedge F_{\text{pb}}.\overrightarrow{y_0}\\&=-h_{3}.F_{\text{pb}}.\overrightarrow{x_0}-L.F_{\text{pb}}.\overrightarrow{z_0}\end{align*}\)

\(\begin{align*}\overrightarrow{\mathcal{M}}(C,{eau} \rightarrow {safran})&=\overrightarrow{\mathcal{M}}(A,{eau} \rightarrow {safran})+\overrightarrow{CA} \wedge \vec{F}({eau} \rightarrow {safran})\\&=\overrightarrow{0}+(-(h_1+h_{2}).\overrightarrow{z_0}+l.\overrightarrow{x_0}) \wedge F_{\text{es}}.\overrightarrow{y_0}\\&=(h_{1}+h_{2}).F_{\text{es}}.\overrightarrow{x_0}+l.F_{\text{es}}.\overrightarrow{z_0}\end{align*}\)

D'où , les deux équations vectorielles issues du PFS :

  • TRS : \(\overrightarrow{F} \left({0} \rightarrow {1} \right)+\overrightarrow{F} \left({pilote} \rightarrow {barre} \right)+\overrightarrow{F} \left({eau} \rightarrow {safran} \right)=\overrightarrow{0}\)

  • TMS au point C : \(\overrightarrow{\mathcal{M}}(C,{0} \rightarrow {1})+\overrightarrow{\mathcal{M}}(C,{pilote} \rightarrow {barre})+\overrightarrow{\mathcal{M}}(C,{eau} \rightarrow {safran})=\overrightarrow{0}\)

Ces deux équations sont projetées sur les 3 axes de la base \((\vec{x_0},\vec{y_0},\vec{z_0})\) :

  • TRS sur \(\vec{x_0}\) : \(X_{01}=0\)

  • TRS sur \(\vec{y_0}\) : \(Y_{01}+F_{\text{pb}}+F_{\text{es}}=0\)

  • TRS sur \(\vec{z_0}\) : \(Z_{01}=0\)

  • TMS en C sur \(\vec{x_0}\) : \(L_{01}-h_{3}.F_{\text{pb}}+(h_{1}+h_{2}).F_{\text{es}}=0\)

  • TMS en C sur \(\vec{y_0}\) : \(M_{01}+F_{\text{pb}}+F_{\text{es}}=0\)

  • TMS en C sur \(\vec{z_0}\) : \(0-L.F_{\text{pb}}+l.F_{\text{es}}=0\)

On obtient bien 6 équations scalaires.

Question

Quelle est l'équation permettant de déterminer l'intensité de l'effort \(\overrightarrow{F}(\text{pilote} \rightarrow \text{barre})\) (équation en résultante ? en moment ? en quel point ?) ? En observant la forme du torseur d'actions mécaniques transmissibles de la liaison équivalente écrit précédemment, conclure sur la stratégie de résolution qu'il aurait fallu proposer pour obtenir le même résultat à partir de l'écriture d'une seule équation scalaire ? Donner l'expression analytique de la norme de l'effort \(\overrightarrow{F}(\text{pilote} \rightarrow \text{barre})\).

Solution

L'équation utile pour déterminer l'intensité de l'effort \(\overrightarrow{F}(\text{pilote} \rightarrow \text{barre})\) est l'équation en moment au point C en projection sur l'axe \(\vec{z_0}\). En effet, c'est la seule équation ne faisant pas intervenir les inconnues de la liaison pivot 0/1. On aurait pu anticiper et n'écrire que cette équation en exploitant le 0 dans le torseur d'actions mécaniques transmissibles de la liaison pivot (0 de la composante sur \(\vec{z_0}\) du moment au point C).

On alors : \(\Vert\overrightarrow{F}(\text{pilote} \rightarrow \text{barre})\Vert=F_{\text{pb}}=l/L.F_{\text{es}}=440N\).