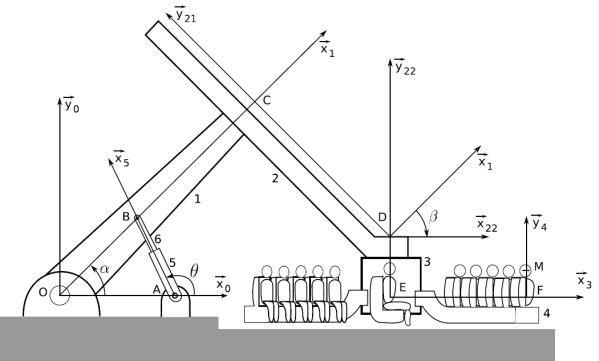
Cas du manège à sensations
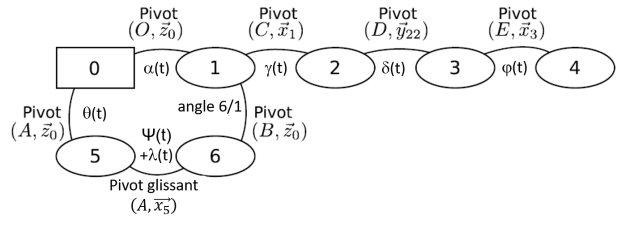
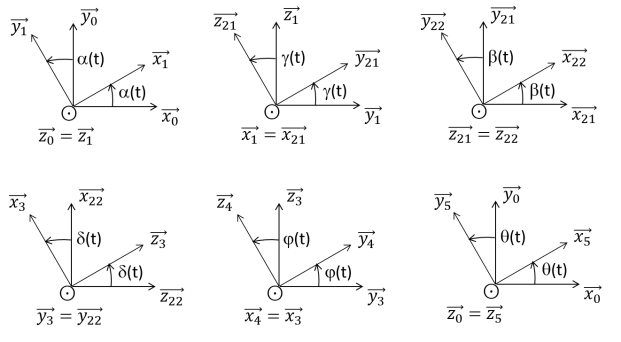
On rappelle le paramétrage du modèle du manège donné précédemment et les figures planes de changement de base réalisées dans le premier polycopié.
Question
Donner l'expression des vecteurs vitesse de rotation suivants :
\(\vec{\Omega}(1/0)\)
\(\vec{\Omega}(5/0)\)
\(\vec{\Omega}(2/1)\)
\(\vec{\Omega}(3/2)\)
\(\vec{\Omega}(4/3)\)
Solution
\(\vec{\Omega}(1/0)=\dot{\alpha}.\vec{z_0}\)
\(\vec{\Omega}(5/0)=\dot{\theta}.\vec{z_0}\)
\(\vec{\Omega}(2/1)=\dot{\gamma}.\vec{x_1}\)
\(\vec{\Omega}(3/2)=\dot{\delta}.\vec{y_{22}}\)
\(\vec{\Omega}(4/3)=\dot{\varphi}.\vec{x_3}\)
Question
Calculer le vecteur vitesse du point C par rapport au référentiel 0
Solution
\(\overrightarrow{V}\left(C/0 \right)=\left(\frac{d\overrightarrow{OC}}{dt}\right)_{0}=\left(\frac{d (c.\vec x_1)}{dt}\right)_{0}=c.\left(\frac{d \vec x_1}{dt}\right)_{0}\)
Pour dériver le vecteur \(\vec{x_1}\) qui n'est pas constant par rapport au référentiel 0, on utilise la formule de Bour vue au début de ce polycopié :
\(\left.\frac{d\vec{x_1}}{dt}\right|_{0}=\left.\frac{d\vec{x_1}}{dt}\right|_{1}+\overrightarrow{\Omega}(1/0)\wedge \vec{x_1}\)
\(\left.\frac{d\vec{x_1}}{dt}\right|_{1}=\vec{0}\) car le vecteur \(\vec{x_1}\) est constant par rapport à la base 1
\(\vec{\Omega}(1/0)=\dot{\alpha}.\vec{z_0}\) (calculé dans l'exercice précédent)
D'où :
\(\left.\frac{d\vec{x_1}}{dt}\right|_{0}=\dot{\alpha}.\vec{z_0}\wedge \vec{x_1}=\dot{\alpha}.\vec{y_1}\) et \(\overrightarrow{V}\left(C/0 \right)=c.\dot{\alpha}.\vec{y_1}\)
Question
Calculer le vecteur vitesse du point B par rapport au solide 5
Solution
\(\overrightarrow{V}\left(B/5 \right)=\left(\frac{d\overrightarrow{AB}}{dt}\right)_{5}=\left(\frac{d (\lambda.\vec x_5)}{dt}\right)_{5}=\dot{\lambda}.\vec{x_5}\) car le vecteur \(\vec{x_5}\) est constant par rapport au référentiel 5.
Question
Calculer le vecteur vitesse du point D par rapport au solide 1.
Solution
Calcul du vecteur vitesse du point D par rapport au solide 1 :
\(\overrightarrow{V}\left(D/1 \right)=\left(\frac{d\overrightarrow{CD}}{dt}\right)_{1}=\left(\frac{d (-d.\vec y_{21})}{dt}\right)_{1}=-d.\left(\frac{d \vec y_{21}}{dt}\right)_{1}\)
On dérive le vecteur \(\vec{y_{21}}\) par rapport au repère 1 :
\(\left.\frac{d\vec{y_{21}}}{dt}\right|_{1}=\left.\frac{d\vec{y_{21}}}{dt}\right|_{2}+\overrightarrow{\Omega}(2/1)\wedge \vec{y_{21}}\)
\(\left.\frac{d\vec{y_{21}}}{dt}\right|_{2}=\vec{0}\) car le vecteur \(\vec{y}_{21}\) est constant par rapport à la base 2
\(\vec{\Omega}(2/1)=\dot{\gamma}.\vec{x_1}\) (calculé dans l'exercice précédent)
D'où :
\(\left.\frac{d\vec{y_{21}}}{dt}\right|_{1}=\dot{\gamma}.\vec{x_1}\wedge \vec{y_{21}}=\dot{\gamma}.\vec{z_{21}}\) et \(\overrightarrow{V}\left(D/1 \right)=-d.\dot{\gamma}.\vec{z_{21}}\)
Question
Déterminer l'accélération du point C par rapport au référentiel 0
Solution
\(\overrightarrow{\Gamma}\left( C/0 \right)=\left(\frac{d\overrightarrow{V}\left( C/0 \right)}{dt}\right)_{0}=\left(\frac{d(c.\dot{\alpha}.\vec{y_1})}{dt}\right)_{0}=c.\left(\frac{d(\dot{\alpha}.\vec{y_1})}{dt}\right)_{0}\) (car \(c\) est une distance constante).
Comme \(\dot{\alpha}\) est une fonction du temps et que le vecteur \(\vec{y_1}\) est variable par rapport au référentiel 0, on doit dériver un produit, soit :
\(\overrightarrow{\Gamma}\left( C/0 \right)=c.\left[\ddot{\alpha}.\vec{y_1}+\dot{\alpha}.\left(\frac{d\vec{y_1}}{dt}\right)_{0}\right]\)
Avec : \(\left(\frac{d\vec{y_1}}{dt}\right)_{0}=\left(\frac{d\vec{y_1}}{dt}\right)_{1}+\overrightarrow{\Omega}(1/0)\wedge \vec{y_1}=-\dot{\alpha}.\vec{x_1}\)
D'où :
\(\overrightarrow{\Gamma}\left( C/0 \right)=c.(\ddot{\alpha}.\vec{y_1}-\dot{\alpha}^2.\vec{x_1})\)