Vecteur vitesse d'un point dans un référentiel donné
Soit le point M et deux repères \(R_i\) et \(R_k\), définis selon la figure ci-dessous. Le point M n'est lié à aucun des deux repères, il est donc possible d'étudier son mouvement par rapport au repère \(R_i\) et/ou au repère \(R_k\).
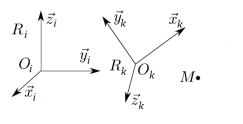
Par définition, la vitesse d'un point M par rapport au référentiel \[R_k\left(O_k,\vec{x_k},\vec{y_k},\vec{z_k}\right)\] est égale à la dérivée du vecteur position \(\overrightarrow{O_k M(t)}\) en utilisant la base \({B_k}\) comme base de dérivation :
De même, par définition, la vitesse d'un point M par rapport à un référentiel \[R_i\left(O_i,\vec{x_i},\vec{y_i},\vec{z_i}\right)\] est égale à la dérivée du vecteur position \(\overrightarrow{O_i M(t)}\) en utilisant la base \({B_i}\) comme base de dérivation :
Remarque :
Le vecteur vitesse du point M à l'instant t par rapport à un repère donné est tangent à la trajectoire au point M(t) dans ce même repère.
Lors du calcul du vecteur vitesse d'un point par rapport à un référentiel donné, le vecteur position qui sera dérivé doit avoir pour point origine un point fixe dans ce référentiel.
Lorsque l'on dérive un vecteur, il est indispensable de préciser la base de dérivation (cf. paragraphe « Quelques notions indispensables...»). Lors du calcul du vecteur vitesse d'un point par rapport à un référentiel donné, la base de dérivation est la base associée à ce référentiel.