Propriétés de la transformée de Laplace

Transformée de Laplace de la dérivée d'une fonction.

On admettra pour toute la suite de ce chapitre les notations et hypothèses suivantes :

\(f\) est une fonction réelle de la variable réelle \(t\)

\(f\) est une fonction causale (nulle pour \(t <0\))

\(F = L[ f ]\) est sa transformée de Laplace, fonction complexe de la variable complexe \(p=\alpha+j \cdot \omega\)

\(f\) et \(L[ f ]\) existent

On montre alors que \(L\left[\frac{df}{dt}\right]\), la transformée de Laplace de la dérivée de \(f\) , s'exprime par :

\[L\left[\frac{df}{dt}\right]=p \cdot L\left[f\right]-f(0^+)=p \cdot F(p)-f(0^+)\]

De même, on montre que \(L\left[\frac{d^2f}{dt^2}\right]\), la transformée de Laplace de la dérivée seconde de \(f\) , s'exprime par :

\[L\left[\frac{d^2f}{dt^2}\right]=p^2 \cdot L\left[f\right]-p \cdot f(0^+)-f^{(1)}(0^+)=p^2 \cdot F(p)-p \cdot f(0^+)-f^{(1)}(0^+)\]

Après généralisation à l'ordre k, on obtient :

\[L\left[\frac{d^kf}{dt^2k}\right]=p^k \cdot F(p)-\sum_{i=0}^{k-1} p^i \cdot f^{(k-1-i)}(0^+)\]

Fondamental

On retrouve dans cette expression les valeurs initiales (à \(t =0\)) de la fonction \(f\) et de ses dérivées successives jusqu'à l'ordre inférieur à l'ordre de dérivation (\(k–1\)). Dans le cas où ces conditions initiales sont nulles, l'expression se simplifie.

\[L\left[\frac{d^kf}{dt^k}\right]=p^k \cdot F(p)\]

FondamentalTransformée de Laplace de la primitive d'une fonction.

En utilisant le résultat précédent, on peut montrer que la transformée de Laplace de la primitive de \(f\) est :

\[G(p)=L\left[\int_0^t f(\tau) \cdot d\tau \right]=\frac{F(p)}{p}\]

Cette propriété n'est valable que pour une intégration de \(0\) à \(t\) de la fonction \(f\).

Théorème du retard

Si \(g\) est la fonction retardée d'un temps \(\tau\) de la fonction \(f\), c'est-à-dire \(g(t)=f(t-\tau)\) alors :

\[ G(p)= L[g(t)]=L[f(t-\tau)]=e^{-\tau \cdot p} \cdot F(p)\]

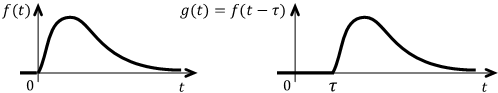
FondamentalThéorème de la valeur initiale

Sous l'hypothèse supplémentaire que \(\lim\limits_{t \rightarrow 0} f(t)\) existe, la valeur initiale de \(f(t)\) peut se calculer à l'aide de la transformée de Laplace \(F\) de \(f\) :

\[\lim\limits_{t \rightarrow 0} f(t)=\lim\limits_{p \rightarrow +\infty} p \cdot F(p)\]

FondamentalThéorème de la valeur finale

Sous les hypothèses supplémentaires que \(\lim\limits_{t \rightarrow +\infty} f(t)\) existe, c'est-à-dire si le système est stable, la limite à la convergence en temps de la fonction \(f\) peut se calculer à l'aide de la transformée de Laplace :

\[\lim\limits_{t \to +\infty} f(t)=\lim\limits_{p \rightarrow 0} p \cdot F(p)\]

Remarque

Il est indispensable de vérifier la stabilité du système étudié avant de chercher à appliquer le théorème de la valeur finale.