Définition des performances d'un système de commande
Le fonctionnement d'un système automatique est caractérisé par un certain nombre de performances. Nous chercherons dans la suite de ce cours (puis en deuxième année) à les prévoir et à les optimiser. Les plus couramment utilisés sont les suivantes :
Définition :
Stabilité : la réponse du système converge-t-elle pour une entrée constante ?
Précision : le système asservi atteint-il la valeur de consigne ?
Rapidité : combien de temps faut-il pour que la réponse du système soit stabilisée ?
Dépassements ou amortissement : la grandeur de sortie a-t-elle tendance à osciller autour de la valeur à convergence avant de l'atteindre ?
Sensibilité aux perturbations : les perturbations extérieures modifient-elles la valeur à convergence de la grandeur asservie ?
Sachant que la réponse dépend évidemment du signal d'entrée, les niveaux de ces performances sont généralement évalués à partir de la réponse à une consigne d'entrée standard : une entrée constante nommée échelon (définie plus en détails dans la suite de chapitre).
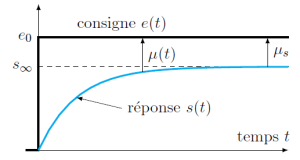
On note alors e(t) le signal d'entrée envoyé comme grandeur consigne et s(t) le signal correspondant alors au signal de la grandeur asservie (cf. figure ci-dessous).
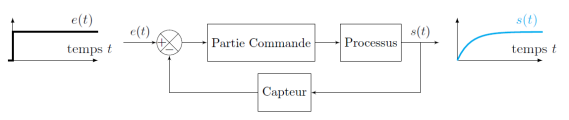
Définition : Stabilité d'un système
Un système asservi est stable si pour toute entrée bornée la sortie est bornée.
Systèmes instables :
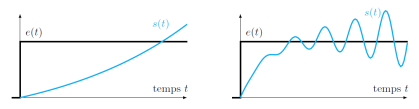
Systèmes stables :
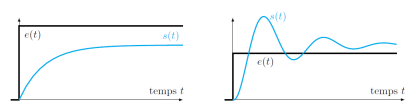
Rapidité d'un système
La rapidité d'un système est le temps que met celui-ci à réagir à une variation brusque de la grandeur d'entrée. Un système est rapide s'il converge en un temps court au regard de son contexte d'utilisation.
Dans la plupart des cas, la valeur finale est atteinte de manière asymptotique, voire oscillante, on retient alors comme principal critère d'évaluation de la rapidité d'un système le temps de réponse à x%. Dans la pratique, c'est le temps de réponse à 5% qui est le plus souvent utilisé.
Définition : Temps de réponse à 5 %
Le temps de réponse à 5%, noté \(t_{5\%}\) correspond au temps mis par le système pour entrer dans une bande de ±5% autour de la valeur à convergence et ne plus en sortir (cf. figure suivante).
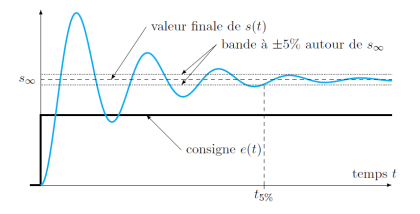
Méthode :
rechercher la valeur asymptotique de la courbe (ne pas confondre avec la consigne qui n'est pas forcément la même) ;
tracer deux droites à ±5% de l'asymptote ;
déterminer l'instant à partir duquel la courbe ne sort plus de la bande à ±5%.
Précision d'un système
La précision qualifie l'aptitude du système à atteindre la valeur de consigne à convergence.
L'erreur \(\mu(t)\) est la différence entre la consigne \(e(t)\) et la sortie \(s(t)\). Elle n'est définie que si la consigne et la sortie sont de même nature (même unité), on a alors : \(\mu(t)=e(t)-s(t)\)
Définition : Erreur statique
L'erreur statique \(\mu_s\) est la limite à convergence de l'erreur pour une entrée e(t) en échelon d'amplitude \(e_0\) (cf. figure ci-dessous) : \(\mu_s=\lim\limits_{t\to\infty}\mu_s(t)=\lim\limits_{t\to\infty}\left(e(t)-s(t)\right)\). Un système est dit parfaitement précis si l'erreur statique est nulle.
Le cahier des charges n'impose pas nécessairement une erreur nulle mais laisse parfois une marge de tolérance définie en %. On doit alors calculer l'erreur statique relative en % en divisant par l'amplitude de l'entrée \(e_0\), soit :
D'où, si l'entrée \(e(t)\) est un échelon d'amplitude \(e_0\) et que le système converge vers une valeur finie (s'il est stable), que l'on note \(s_\infty\), alors : \(\mu_s=e_0-s_\infty\) et \(\mu_s(\%)=\frac{e_0-s_\infty}{e_0}\)
Amortissement d'un système
Un système présente des dépassements si la réponse oscille autour de la valeur à convergence avant de l'atteindre. L'amortissement est alors caractérisé par le rapport entre les amplitudes successives des oscillations de la sortie. Plus ces oscillations s'atténuent rapidement, plus le système est amorti.
Selon le contexte, le cahier des charges peut exiger :
l'absence de dépassement ;
une amplitude maximale des dépassements.

Pour une entrée en échelon e(t), les dépassements sont définis par rapport à la valeur à convergence de la réponse. Ils peuvent être supérieurs ou inférieurs à la valeur à convergence et sont numérotés dans l'ordre croissant d'apparition.
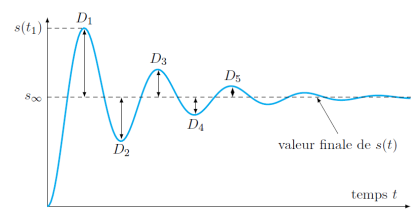
Définition : Dépassements
Les dépassements sont généralement spécifiés en pourcentage de la valeur à convergence. On calcule ainsi le premier dépassement en pourcentage par la formule :
où \(t_1\) est l'instant pour lequel le premier dépassement est atteint et \(s_\infty\) la valeur asymptotique.
Remarque :
Pour certaines applications, un comportement oscillant n'est pas autorisé et tout dépassement est inacceptable (lorsqu'il implique une collision, le débordement d'un fluide lors d'un remplissage,...). Pour d'autres application, un certain pourcentage de dépassement peut être toléré (régulation de température d'une pièce, ...).
Sensibilité aux perturbations
Dans son contexte, le système est piloté par la consigne d'entrée \(e(t)\). Cependant des perturbations extérieures \(p(t)\), cf. figure suivante) non contrôlables peuvent affecter le comportement du système et modifier sa réponse \(s(t)\). Il est souvent nécessaire de vérifier que l'influence des perturbations est limitée et que le système peut s'autocorriger. On parle de sensibilité aux perturbations.
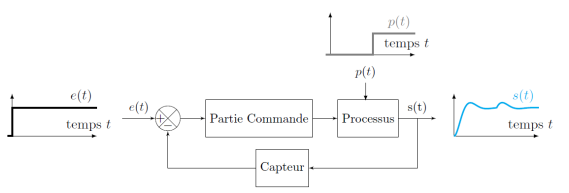
Définition : Sensibilité aux perturbations
Un système est dit sensible aux perturbations s'il ne converge pas vers la même valeur selon qu'une perturbation extérieure s'applique ou pas.
Un système insensible aux perturbations peut voir sa grandeur de sortie évoluer transitoirement lors de l'apparition de la perturbation, mais revenir à sa valeur de convergence ensuite (cf. ci-dessous).