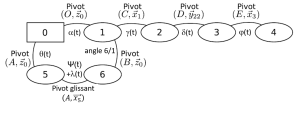
Cas du manège à sensations
Question
Solution
Comme exprimé précédemment, la relation de fermeture cinématique écrite pour le manège à sensations est la suivante :
\(\left\{\mathcal{V}\left(6/5\right)\right\}+\left\{\mathcal{V}\left(5/0\right)\right\}+\left\{\mathcal{V}\left(0/1\right)\right\}+\left\{\mathcal{V}\left(1/6\right)\right\}=\left\{\mathcal{V}\left(6/6\right)\right\}=\left\{0\right\}\)
Tous les torseurs doivent être exprimés au même point pour pouvoir les sommer (on utilise les résultats des précédents exercices traités dans ce polycopié, une partie de ces torseurs ayant déjà été exprimée en un point unique B) :
Torseur \(\left\{\mathcal{V}\left(6/5\right)\right\}\) :
\(\left\{\mathcal{V}\left(6/5\right)\right\}=\left\{ \begin{array}{c} \dot{\psi}.\overrightarrow{x_5} \\\dot{\lambda}.\overrightarrow{x_5} \end{array}\right\}_B\)
Torseur \(\left\{\mathcal{V}\left(5/0\right)\right\}\) :
\(\left\{\mathcal{V}\left(5/0\right)\right\}=\left\{ \begin{array}{c}\dot{\theta}.\overrightarrow{z_0} \\\lambda.\dot{\theta}.\vec{y_5}\end{array}\right\}_B\)
Torseur \(\left\{\mathcal{V}\left(0/1\right)\right\}\) :
\(\left\{\mathcal{V}\left(0/1\right)\right\}=-\left\{\mathcal{V}\left(1/0\right)\right\}=\left\{ \begin{array}{c}-\dot{\alpha}.\overrightarrow{z_0} \\-b.\dot{\alpha}.\vec{y_1} \end{array}\right\}_B\)
Torseur \(\left\{\mathcal{V}\left(1/6\right)\right\}\) : le mouvement de 1 par rapport à 6 est un mouvement de rotation autour de l'axe \((B,\vec{z_0})\), mais l'angle de rotation de 1 par rapport à 6 n'est pas paramétré dans l'énoncé. Il faut donc ajouter une variable. On note \(\epsilon\) cet angle.
D'où, \(\left\{\mathcal{V}\left(1/6\right)\right\}=\left\{ \begin{array}{c}\dot{\epsilon}.\overrightarrow{z_0} \\\vec{0} \end{array}\right\}_B\)
On exprime alors la somme torsorielle :
\(\left\{\mathcal{V}\left(6/5\right)\right\}+\left\{\mathcal{V}\left(5/0\right)\right\}+\left\{\mathcal{V}\left(0/1\right)\right\}+\left\{\mathcal{V}\left(1/6\right)\right\}=\left\{0\right\}\)
\(\left\{ \begin{array}{c} \dot{\psi}.\overrightarrow{x_5} \\\dot{\lambda}.\overrightarrow{x_5} \end{array}\right\}_B+\left\{ \begin{array}{c}\dot{\theta}.\overrightarrow{z_0} \\\lambda.\dot{\theta}.\vec{y_5}\end{array}\right\}_B+\left\{ \begin{array}{c}-\dot{\alpha}.\overrightarrow{z_0} \\-b.\dot{\alpha}.\vec{y_1} \end{array}\right\}_B+\left\{ \begin{array}{c}\dot{\epsilon}.\overrightarrow{z_0} \\\vec{0} \end{array}\right\}_B=\left\{ \begin{array}{c} \overrightarrow{0} \\\overrightarrow{0} \end{array}\right\}_B\)
On en déduit deux relations vectorielles :
\(\dot{\psi}.\overrightarrow{x_5}+\dot{\theta}.\overrightarrow{z_0}-\dot{\alpha}.\overrightarrow{z_0}+\dot{\epsilon}.\overrightarrow{z_0}=\overrightarrow{0}\) notée (1)
\(\dot{\lambda}.\overrightarrow{x_5}+\lambda.\dot{\theta}.\vec{y_5}-b.\dot{\alpha}.\vec{y_1}+\overrightarrow{0}=\overrightarrow{0}\) notée (2)
Chacune de ces relations peuvent être projetées sur les 3 axes d'une base orthonormée, par exemple la base 0 :
(1) projetée sur \(\vec{x_0}\) : \(\dot{\psi}\cdot\cos\theta=0\), soit \(\dot{\psi}=0\)
(1) projetée sur \(\vec{y_0}\) : \(\dot{\psi}\cdot\sin\theta=0\), on retrouve bien \(\dot{\psi}=0\)
(1) projetée sur \(\vec{z_0}\) : \(\dot{\theta}-\dot{\alpha}+\dot{\epsilon}=0\), soit \(\dot{\epsilon}=\dot{\alpha}-\dot{\theta}\)
(2) projetée sur \(\vec{x_0}\) : \(\dot{\lambda}\cdot\cos\theta-\lambda.\dot{\theta}\cdot\sin\theta+b.\dot{\alpha}.\sin\alpha=0\)
(2) projetée sur \(\vec{y_0}\) : \(\dot{\lambda}\cdot\sin\theta+\lambda.\dot{\theta}\cdot\cos\theta-b.\dot{\alpha}.\cos\alpha=0\)
(2) projetée sur \(\vec{z_0}\) : \(0=0\)
Nous obtenons bien 4 relations utiles entre 5 paramètres cinématiques. Tous peuvent donc être exprimés en fonction de l'entrée du système \(\dot{\theta}\).
Question
En déduire la loi entrée/sortie reliant la vitesse de rotation du bras 1 par rapport au sol 0 et la vitesse de translation de la tige du vérin 6 par rapport au corps du vérin 5 : \(\dot{\alpha}=f\left(\dot{\lambda}\right)\) indépendamment des autres paramètres cinématiques (\(\dot{\psi}\), \(\dot{\theta}\), \(\dot{\epsilon}\))
Solution
On utilise deux des relations issues de la question précédentes : (2) projetée sur \(\vec{x_0}\), notée (2x) et (2) projetée sur \(\vec{y_0}\), notée (2y)
(2x) donne : \(\lambda.\dot{\theta}.sin\theta=\dot{\lambda}.cos\theta+b.\dot{\alpha}.sin\alpha\)
(2y) donne : \(\lambda.\dot{\theta}.cos\theta=b.\dot{\alpha}.cos\alpha-\dot{\lambda}.sin\theta\)
En écrivant le quotient (2x)/(2y), on obtient une relation entre \(\dot{\lambda}\) et \(\dot{\alpha}\) indépendamment de \(\dot{\theta}\) :
\(tan\theta=\frac{b.\dot{\alpha}.sin\alpha+\dot{\lambda}.cos\theta}{b.\dot{\alpha}.cos\alpha-\dot{\lambda}.sin\theta}\)
Après calculs, on obtient :
\(\dot{\alpha}=\frac{\dot{\lambda}}{b}.\frac{cos\theta+sin\theta.tan\theta}{\cos\alpha.tan\theta-sin\theta}\)