Loi E/S cinématique
Cas d'une chaîne ouverte
Dans le cas d'une chaîne ouverte, les mouvements des liaisons sont tous indépendants les uns des autres. La mobilité du système est alors égale à la somme des degrés de liberté de chacune des liaisons.
La vitesse de n'importe que point du mécanisme peut être obtenue par dérivation du vecteur position correspondant. Il est aussi possible d'utiliser la composition des torseurs cinématiques.
Exemple : Cas du manège à sensations
Dans le cas du manège traité précédemment, les solides 1-2-3-4 forment une chaîne ouverte.
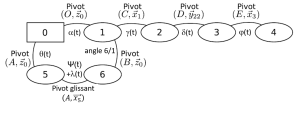
Il est alors possible d'exprimer le torseur du mouvement de 4 par rapport à 1 par composition des torseurs :
\(\left\{\mathcal{V}\left(4/0\right)\right\}=\left\{\mathcal{V}\left(4/3\right)\right\}+\left\{\mathcal{V}\left(3/2\right)\right\}+\left\{\mathcal{V}\left(2/1\right)\right\}+\left\{\mathcal{V}\left(1/0\right)\right\}\)
Le fait de déterminer le torseur \(\left\{\mathcal{V}\left(4/0\right)\right\}\) permet ensuite de calculer la vitesse de n'importe quel point appartenant au solide 4 par rapport au sol en fonction des paramètres cinématiques de toutes les liaisons de la chaîne ouverte.
Cas d'une chaîne fermée
Une chaîne fermée est constituée d'un ensemble de solides reliés par de multiples liaisons. L'assemblage forme une ou plusieurs boucles et les paramètres cinématiques sont dépendants les uns des autres.
Le mécanisme étant motorisé au niveau de certaines liaisons (où le mouvement est donc connu), on recherche le mouvement d'une ou plusieurs autres liaisons : on parle de(s) « loi(s) entrée-sortie » du mécanisme.
Exemple : Cas du manège à sensations
Dans le cas du manège traité précédemment, les solides 0-1-5-6-0 forment une chaîne fermée.
La liaison "motorisée" est la liaison 5/6, grace au vérin (translation), dont on connaît alors la vitesse.
La liaison dont on recherche le mouvement est la liaison 1/0 (vitesse de rotation du bras 1 par rapport au sol)
Les autres degrés de liberté des liaisons ne sont ni connus ni recherchés, mais il serait possible de les exprimer eux-aussi en fonction de la vitesse d'élongation du vérin.
Le graphe de liaison ci-contre montre qu'il existe une seule chaine fermée dans le mécanisme du manège.
Définition : Nombre cyclomatique
Dans le cas d'un mécanisme en chaîne fermée, on appelle cycle, un chemin fermé du graphe ne passant pas deux fois par le même sommet. Parmi les cycles qui peuvent être mis en évidence dans un graphe, un certain nombre sont indépendants. Leur nombre \(\mu\) appelé aussi nombre cyclomatique peut être calculé par la relation : \(\mu=n_L-n_P+1\), avec \(n_L\)=nombre de liaison et \(n_P\)=nombre de solides (bati compris).
La mise en évidence des cycles indépendants est particulièrement intéressante pour étudier le comportement géométrique et cinématique d'un mécanisme. Dans le cas d'un mécanisme en chaîne fermée, le nombre cyclomatique traduit le nombre de relations de fermetures cinématiques qu'il est possible de réaliser.
Définition : Fermeture cinématique
Une relation de fermeture cinématique est une somme de torseur égale au torseur nul, écrite par composition des mouvements dans une chaîne cinématique fermée.
A partir de cette somme torsorielle, il est possible d'écrire 2 relations vectorielles (une relation portant sur les vecteurs vitesse de rotation et une relation portant sur les vecteurs vitesse). Ces 2 relations vectorielles peuvent ensuite être projetées sur les 3 vecteurs d'une base orthonormée, et permettent donc d'obtenir 6 relations scalaires. Ce sont ces relations qui permettent d'exprimer les paramètres cinématiques les uns en fonction des autres.
Exemple : Cas du manège à sensations
La relation de fermeture cinématique écrite pour le manège à sensations est la suivante :
\(\left\{\mathcal{V}\left(6/5\right)\right\}+\left\{\mathcal{V}\left(5/0\right)\right\}+\left\{\mathcal{V}\left(0/1\right)\right\}+\left\{\mathcal{V}\left(1/6\right)\right\}=\left\{\mathcal{V}\left(6/6\right)\right\}=\left\{0\right\}\)
Attention :
La fermeture cinématique doit scrupuleusement respecter la composition des vitesses afin que la somme des torseurs soit bien égale au torseur nul.