Cinématique du contact ponctuel entre solides
Vitesse de glissement
Soient deux solides \(S_i\) et \(S_k\) en contact par les surfaces (\(\Sigma_i\) ) et (\(\Sigma_k\) ) qui les limitent et \(R_i\) et \(R_k\) les repères respectivement associés à ces solides.
Les deux surfaces sont tangentes en un point I et le contact est ponctuel. On note (\(\pi\)) le plan tangent commun aux deux solides au point I et \(\vec{n}\) le vecteur normal à ce plan passant par I.
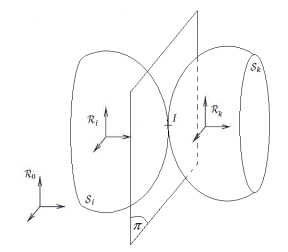
Définition : Vitesse de glissement
On appelle vitesse de glissement du solide \(S_k\) par rapport au solide \(S_i\), dans le repère \(R_o\), au point \(I\) le vecteur :
Remarque : La vitesse de glissement est indépendante du repère de référence.
En effet nous pouvons écrire :
\(\overrightarrow{G}_{/R_0}(I)=\overrightarrow{V}(I \in S_k/R_0)-\overrightarrow{V}(I \in S_i/R_0)=\overrightarrow{V}(I \in S_k/S_i)\)
\(\overrightarrow{G}_{/R_n}(I)=\overrightarrow{V}(I \in S_k/R_n)-\overrightarrow{V}(I \in S_i/R_n)=\overrightarrow{V}(I \in S_k/S_i)\)
Donc :
\(\overrightarrow{G}_{/R_0}(I)=\overrightarrow{G}_{/R_1}(I)=\ldots=\overrightarrow{G}_{/R_n}(I)\)
C'est pourquoi la vitesse de glissement est notée \(\overrightarrow{V}(I \in S_k/S_i)\).
Remarque : La vitesse de glissement du solide Sk par rapport au solide Si, au point I, est contenue dans le plan tangent commun (π).
Soit I le point géométrique de contact. Au cours du mouvement, le point I se déplace sur les solides \(S_i\) et \(S_k\). Il décrit sur \(S_i\) une courbe (\(C_i\)) et sur \(S_k\) une courbe (C\(_k\)).
Nous savons que :
\(\overrightarrow{V}(I/S_i)\) est porté par la tangente à (\(C_i\)) en I,
\(\overrightarrow{V}(I/S_k)\) est porté par la tangente à (C\(_k\)) en I.
De plus ces deux tangentes sont dans le plan tangent commun aux deux solides \(S_i\) et \(S_k\) au point I.
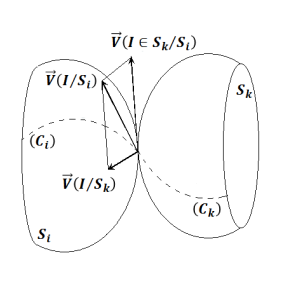
Or, d'après la composition des vitesses au point I, nous avons : \(\overrightarrow{V}(I/S_i)=\overrightarrow{V}(I \in S_k/S_i)+\overrightarrow{V}(I/S_k)\). Ces trois vecteurs sont donc coplanaires (car les trois côtés d'un triangle sont dans un même plan).
Ceci implique bien que la vitesse de glissement \(\overrightarrow{V}(I \in S_k/S_i)\) appartient au plan tangent commun aux solides \(S_i\) et \(S_k\) au point I.
Remarque sur la condition cinématique de maintien du contact : si le vecteur vitesse de glissement \(\overrightarrow{V}(I \in S_k/S_i)\) n'appartient pas au plan tangent commun aux solides \(S_i\) et \(S_k\) au point I, alors, cela signifie que les solides \(S_i\) et \(S_k\) s'éloignent ou s'interpénètrent. Dans ce cas-là, le maintien du contact entre les solides au cours du temps n'est pas assuré.
La condition cinématique de maintien du contact s'écrit donc : \(\overrightarrow{V}(I \in S_k/S_i)\cdot\vec{n}=0\).
Fondamental : Roulement sans glissement
Dans les mécanismes de transformation de mouvement, on rencontre très fréquemment le fonctionnement en conditions de roulement sans glissement (contact d'une roue sur le sol, engrènement, ...). La condition cinématique de roulement sans glissement du solide \(S_k\) par rapport au solide \(S_i\) s'écrit : \(\overrightarrow{V}(I \in S_k/S_i)=\vec{0}\).