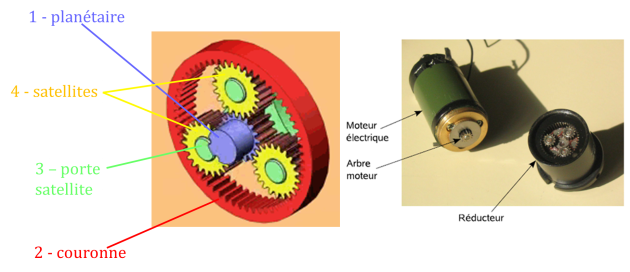
Trains épicycloïdaux
Les trains épicycloïdaux sont des trains d'engrenages particuliers : l'axe de rotation de certains pignons est mobile. On trouve ce type d'engrenage dans bon nombre de réducteur à forte réduction et faible encombrement (par exemple sur la plate-forme Stewart du labo de SII). Les boîtes de vitesses automatiques disposent elles aussi de trains épicycloïdaux.
Cas d'école :
On étudie le train épicycloïdal de la ci-dessous. On appelle 1 le planétaire, 2 la couronne (parfois aussi appelée planétaire extérieur), 3 le porte-satellite et 4 le satellite.
Sur le schéma cinématique, on retrouve les 4 solides mobiles. Un seul satellite parmi les 3 est représenté car ils sont redondants d'un point de vue cinématique (il y en a trois pour répartir les efforts).
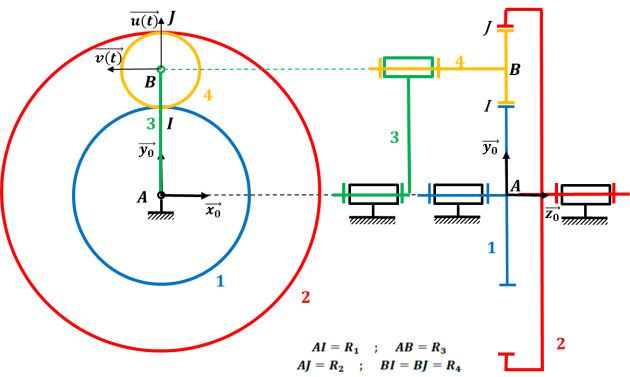
On remarque qu'en plaçant le repère de l'observateur accroché au porte-satellite (3), le train est réduit à un train simple (à axes fixes).
Schéma cinématique en choisissant le bâti (0) comme référentiel | Schéma cinématique en choisissant le porte-satellite (3) comme référentiel |
Les relations établies précédemment permettent alors de déterminer le rapport de transmission en fonction du nombre de dents, lorsque l'observateur est « accroché » à 3 :
\(\frac{\omega_{2/3}}{\omega_{1/3}}=-\frac{R_1}{R_4}\frac{R_4}{R_2}=-\frac{R_1}{R_2}\)
On en déduit une relation appelée relation de Willis :
La constante λ est appelée raison du train.
Nous obtenons donc une relation (la relation de Willis) entre trois paramètres cinématiques (la mobilité du système est bien égale à deux). Parmi ces trois paramètres, il est nécessaire d'en fixer un pour déterminer la loi entrée/sortie (ou le rapport de transmission) du train épicycloïdal, qui relie les deux autres paramètres (vitesse de rotation de l'arbre d'entrée et vitesse de rotation de l'arbre de sortie).
Un même train épicycloïdal peut donc être utilisé dans différentes configurations, avec différents rapports de transmission (quelques exemples ci-dessous) :
Cas 1 | Cas 2 | Cas 3 | |
|---|---|---|---|
Solide fixe par rapport à 0 | Planétaire (1) | Couronne (2) | Porte satellite (3) |
Loi entrée/sortie | \(\frac{\omega_{2/0}-\omega_{3/0}}{-\omega_{3/0}}=\lambda=-\frac{R_1}{R_2}\) | \(\frac{-\omega_{3/0}}{\omega_{1/0}-\omega_{3/0}}=\lambda=-\frac{R_1}{R_2}\) | \(\frac{\omega_{2/0}}{\omega_{1/0}}=\lambda=-\frac{R_1}{R_2}\) |
rapport de transmission | \(r=(1-\lambda)\) ou \(r=\frac{1}{(1-\lambda)}\) | \(r=-\frac{\lambda}{(1-\lambda)}\) ou \(r=-\frac{(1-\lambda)}{\lambda}\) | \(r=\lambda\) ou \(r=\frac{1}{\lambda}\) |