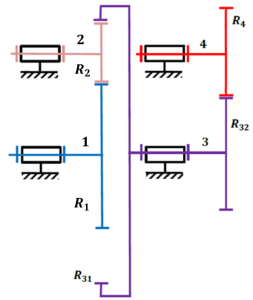
Trains d'engrenages à axes fixes
Question
En utilisant les résultats démontrés précédemment pour un engrenage à denture droite extérieure et intérieure, retrouver le rapport de transmission de ce train d'engrenages .
Solution
\(\frac{\omega_{20}}{\omega_{10}}=-\frac{R_1}{R_2}\)
\(\frac{\omega_{30}}{\omega_{20}}=\frac{R_2}{R_{31}}\)
\(\frac{\omega_{40}}{\omega_{30}}=-\frac{R_{32}}{R_4}\)
donc en multipliant tous les termes :
\(\frac{\omega_{40}}{\omega_{10}}=\frac{R_1}{R_2}\cdot\frac{R_2}{R_{31}}\cdot\frac{R_{32}}{R_4}\)
Ce résultat peut être généralisé à un train comportant n engrenages en série :
\[r=\frac{\omega_N}{\omega_1}=(-1)^n\frac{Z_1\cdot Z_3\dots Z_{N-1}}{Z_2\cdot Z_4\dots Z_{N}}\] où n est le nombre de contact extérieur. Ce qui peut se formuler :
\[r=\frac{\omega_N}{\omega_1}=(-1)^n\frac{\text{produit du nombre de dents des roues menantes}}{\text{produit du nombre de dents des roues menées}}\\ \\
r=\frac{\omega_N}{\omega_1}=(-1)^n\frac{\text{produit du rayon des roues menantes}}{\text{produit du rayon des roues menées}}\]