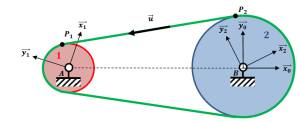
Système poulie-courroie
Hypothèses :
La courroie ne glisse pas sur les poulies,
La courroie est inextensible,
Poulie motrice 1 de rayon \(R_1\),
Poulie réceptrice 2 de rayon \(R_2\).
Selon l'hypothèse que la courroie ne se déforme pas, on a : \(\overrightarrow{V}(P_1 \in courroie/0)=\overrightarrow{V}(P_2 \in courroie/0)\)
Selon l'hypothèse que la courroie ne glisse pas sur les poulies, on a : \(\overrightarrow{V}(P_1 \in courroie/0)=\overrightarrow{V}(P_1 \in 1/0)\) et \(\overrightarrow{V}(P_2 \in courroie/0)=\overrightarrow{V}(P_2 \in 2/0)\), avec \(\left\|\overrightarrow{V}(P_1 \in 1/0)\right\|=\left\|\overrightarrow{P_1A}\wedge\overrightarrow{\Omega}_{1/0}\right\|=R_1\cdot \omega_{10}\) et \(\left\|\overrightarrow{V}(P_2 \in 2/0)\right\|=\left\|\overrightarrow{P_2B}\wedge\overrightarrow{\Omega}_{2/0}\right\|=R_2\cdot \omega_{20}\).
D'où la relation \(R_1\cdot\omega_1=R_2\cdot\omega_2\) et le rapport de réduction r :