Principe
L'étude harmonique d'un système linéaire continu et invariant est l'étude de sa réponse en régime permanent (ou régime établi) à une entrée sinusoïdale \(e(t)=A\cdot\sin(\omega \cdot t)\) (A = amplitude ; ω = pulsation en rad.s-1).
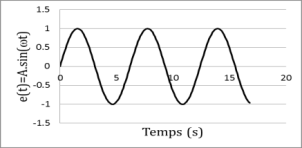
La réponse temporelle à une entrée sinusoïdale d'un système du premier ordre peut donc se décomposer en deux parties (voir ci-dessous :) :
Un régime transitoire, en exponentielle décroissante, dont l'influence disparait quand t>3.τ
Un régime permanent, qualifié aussi de régime forcé car l'entrée sinusoïdale impose une sortie sinusoïdale de même pulsation ω.
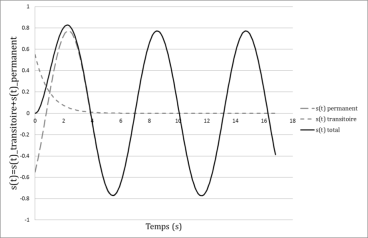
Un système linéaire soumis à ce type de sollicitation sinusoïdale présentera une réponse en régime permanent sinusoïdale, de même pulsation ω, d'amplitude B et avec un éventuel déphasage φ (en rad) :
\(s(t)=B \cdot \sin(\omega\cdot t+\varphi)\)
L'amplitude du signal de sortie B et son déphasage φ sont significatifs du comportement du système et varient en fonction de ω. Pour une pulsation ω donnée, il existe un rapport d'amplitude entre les deux sinusoïdes ainsi qu'un déphasage. Faire l'étude harmonique du système revient à étudier ces variations.
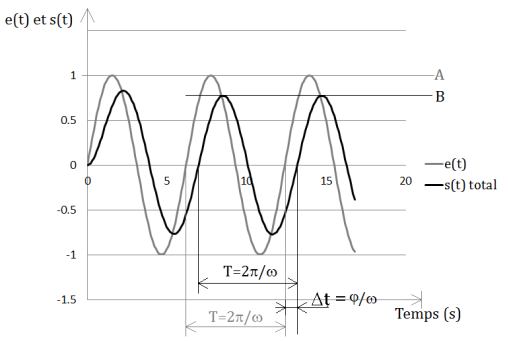
Remarque :
La sortie s(t) est obligatoirement en retard par rapport à l'entrée (si ce n'est pas le cas, le système pourrait prédire l'avenir !). Le déphasage φ(ω) est donc obligatoirement négatif.