Diagramme de Bode
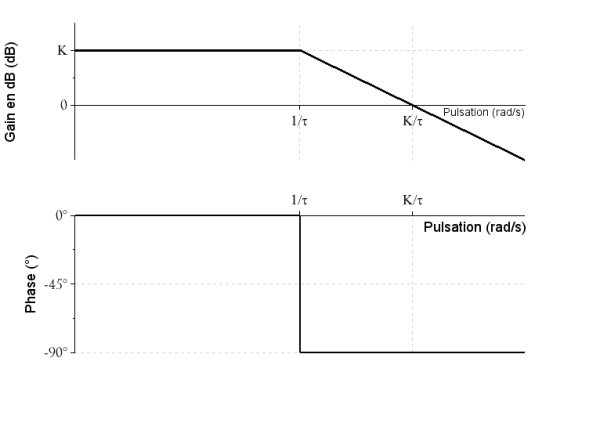
Tracé asymptotique du diagramme de Bode
Si \(\omega \to 0\) alors \(\left\lbrace\begin{array}{l}\left|H(\omega)\right|\approx K \\ \\ \varphi(\omega)\approx 0°\\\end{array}\right.\) donc \(\left\lbrace\begin{array}{l}\left|H(\omega)\right|_{dB}\approx 20\log K \\ \\ \varphi(\omega)\approx 0° \\\end{array}\right.\)
Si \(\omega \to \infty\) alors \(\left\lbrace\begin{array}{l}\left|H(\omega)\right|\approx \frac{K}{\tau.\omega} \\ \\ \varphi(\omega)\approx -90°\\\end{array}\right.\) donc \(\left\lbrace\begin{array}{l}\left|H(\omega)\right|_{dB}\approx 20\log \frac{K}{\tau}-20\log{\omega} \\ \\ \varphi(\omega)\approx -90° \\\end{array}\right.\)
La courbe de gain en décibels du diagramme de Bode d'un système du premier ordre présente une asymptote horizontale à 20.logK lorsque la pulsation est faible et une asymptote oblique de -20 dB par décade de pente (décade : intervalle[ω;10.ω]) lorsque la pulsation est élevée.
Démonstration : \(\left|H(10.\omega)\right|_{dB}\approx 20\log \frac{K}{\tau}-20\log{10.\omega}= 20\log \frac{K}{\tau}-20\log 10 -20\log{\omega}\)
donc \(\left|H(10.\omega)\right|_{dB}=20\log \frac{K}{\tau}-20 -20\log{\omega}=\left|H(\omega)\right|_{dB}-20 dB\)
Remarque :
Les asymptotes à la courbe de gain en décibels d'un diagramme de Bode ont obligatoirement une pente multiple de 20 dB/décade. Nous appellerons pente d'ordre n une pente égale à 20.n dB/décade. Dans le cas du système du premier ordre, l'asymptote en +∞ est donc une pente d'ordre -1.
La courbe de phase du diagramme de Bode d'un système du premier ordre présente une asymptote horizontale à 0° lorsque la pulsation est faible et une asymptote horizontale à -90° lorsque la pulsation est importante.
Les deux asymptotes de la courbe de gain en décibels se croisent en un point dont l'abscisse est \(\omega_c\). Cette pulsation particulière est appelée pulsation de cassure. Cette pulsation \(\omega_c\) est telle que :
\(20\log(K/\tau)-20\log\omega_c=20\log K\) on en déduit \(-20\log\tau-20\log\omega_c=0\) donc \(\omega_c=\frac{1}{\tau}\)
La pulsation de cassure d'un système du premier ordre est \(\omega_c=\frac{1}{\tau}\)
Fondamental : Tracé asymptotique
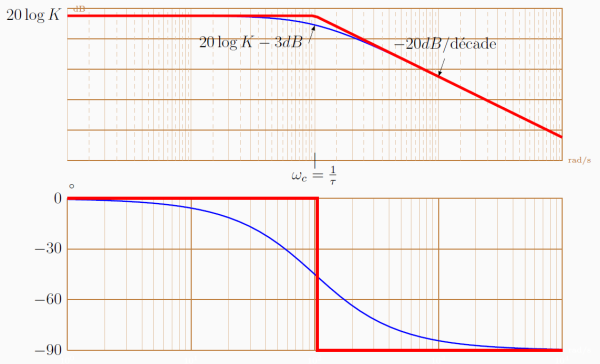
Tracé du diagramme de Bode réel
Le tracé des courbes réels peuvent se faire à partir du tracé asymptotique :
Fondamental :
Les résultats nécessaires au tracé du diagramme de Bode (asymptotique et réel) d'un système du premier ordre standard de fonction de transfert \(H(p)=\frac{K}{1+\tau.p}\) sont regroupés dans le tableau suivant à connaître par cœur. Ces résultats seront utiles pour les cours de physique et de SII.
\(\omega<<\omega_c\) | \(\omega_c=\frac{1}{\tau}\) | \(\omega>>\omega_c\) |
\(\left|H(\omega)\right|_{dB}\approx 20\log K\) \(\varphi(\omega)\approx 0° \) | \(\left|H(\omega_c)\right|_{dB}\approx 20\log K-3dB\) \( \varphi(\omega_c)\approx -45° \) | \(\left|H(\omega)\right|_{dB}\approx 20\log \frac{K}{\tau}-20\log{\omega}\) \(\varphi(\omega)\approx -90°\) |
\(\left|H(\omega)\right|_{dB}\): Asymptote horizontale \(\varphi\): Asymptote horizontale 0° | \(\left|H(\omega)\right|_{dB}\): croisement des asymptotes à la pulsation de cassure \(\omega_c\) \(\varphi=-45°\): | \(\left|H(\omega)\right|_{dB}\): Asymptote oblique de pente -20 dB⁄"décade" \(\varphi\): Asymptote horizontale -90° |
Du fait du tracé en échelle logarithmique, la courbe de gain en décibels reste proche de ses asymptotes sur une grande partie du graphique. Pour positionner plus précisément la courbe de phase réelle, il est possible de déterminer la valeur de la phase pour quelques point intermédiaires :
\(\omega=\frac{0,1}{\tau}\) | \(\omega=\frac{0,2}{\tau}\) | \(\omega=\frac{0,5}{\tau}\) | \(\omega=\frac{1}{\tau}\) | \(\omega=\frac{2}{\tau}\) | \(\omega=\frac{5}{\tau}\) | \(\omega=\frac{10}{\tau}\) |
\(-5,7°\) | \(-11,3°\) | \(-26,6°\) | \(-45°\) | \(-63,4°\) | \(-78,7°\) | \(-84,3°\) |
Méthode : Tracer du diagramme de Bode d'un premier ordre
Identifier K et calculer \(20\log K\).
Identifier \(\tau\) et calculer \(\omega_c=\frac{1}{\tau}\).
Pour le gain : tracer une asymptote horizontale de gain \(20 \log K\) jusqu'à la pulsation \(\omega_c\) puis tracer une asymptote ayant une pente de -\(20dB\) par décade. La courbe réelle passe à -\(3dB\) sous la cassure des asymptotes.
Pour la phase : tracer une asymptote horizontale à \(0°\) jusqu'à la pulsation \(\omega_c\) puis tracer une asymptote horizontale à \(-90°\).
Méthode : Identifier un premier ordre à partir de son diagramme de Bode
Vérifier sur la courbe de gain la pente est de -20dB/décade et que la phase tend vers -90° pour \(\omega\) tendant vers \(+\infty\).
Relever la valeur du gain \(20 \log K\) pour \(\omega\) tendant vers \(0\) et en déduire \(K\).
Trouver l'intersection entre les deux asymptotes de gain, relever \(\omega_c=\dfrac{1}{\tau}\) et en déduire \(\tau\). Autre solution, relever \(\omega_c\).