Boucle fermée - Boucle ouverte
La fonction de transfert en boucle fermée s'écrit :
\(H_{BF}(p)=\frac{A(p)}{1+A(p)C(p)}\)
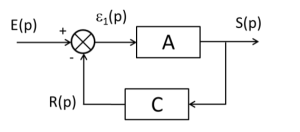
La stabilité de ce système dépend des racines du dénominateur : \(1+A(p)C(p)\). Il faut résoudre l'équation suivante :
La stabilité de la boucle fermée dépend donc de \(A(j\omega).C(j\omega)\) et du point \((-1,0)\) dans le plan complexe.
Rappel :
\(A(p).C(p)\) est la fonction de transfert en boucle ouverte.
Définition : Point Critique
Le point \((-1,0)\) est appelé point critique.
L'´énoncé du critère qui permet de savoir si un système est stable en B.F se réfère donc au point critique. Celui-ci possède un module unitaire et une phase de -180°.
Nous allons définir deux pulsations particulières dans un diagramme de Bode :
Définition : pulsation de coupure des 0dB
On appelle \(\omega_{0dB}\) la pulsation pour laquelle la courbe de gain du diagramme de Bode coupe l'axe des 0 dB. On parlera aussi de pulsation de coupure des 0 dB.
Définition : Pulsation de coupure des -180°
On appellera \(\omega_{-\pi}\) la pulsation pour laquelle la courbe des phases coupe l'axe des -180°.